2023-2024学年广东省深圳市七年级下学期数学期中仿真模拟卷四【范围：1-4章】

试卷更新日期：2024-04-13 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

1. 我国古代数学家祖冲之推算出π的近似值为 $\frac{355}{113} ，$ 它与 π 的误差小于 0.000 000 3. 将0.000 000 3用科学记数法可表示为（）

A、3×10^-⁷ B、 $0.3 \times {10^{-}}^{6}$ C、 $3 \times {10^{-}}^{6}$ D、3×10⁷

查看试题解析
2. $x^{3} \cdot x^{3}$ 的运算结果正确的时（）

A、 $2 x^{3}$ B、 $x^{6}$ C、 $2 x^{6}$ D、 $x^{9}$

查看试题解析
3. 现有2cm，3cm，5cm，6cm长的四根木棒，任选其中的三根组成三角形，那么可以组成三角形的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，将一个三角板 $60 °$ 角的顶点与另一个三角板的直角顶点重合， $∠ 1 = 27 °$ ， $∠ 2$ 的大小是（）

A、 $27 °$ B、 $57 °$ C、 $58 °$ D、 $60 °$

查看试题解析
5. 如图，点 $E$ 在线段BC的延长线上，下列四个结论中正确的个数是（）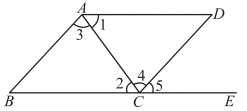
①如果 $∠ 3 = ∠ 4$ ，那么 $A D / / B C$
②如果 $∠ 1 = ∠ 2$ ，那么 $A D / / B C$
③如果 $A D / / B C$ ，那么 $∠ D + ∠ B C D = 18 0^{°}$
④如果 $A B / / D C$ ，那么 $∠ B = ∠ 5$

A、1 B、2 C、3 D、4

查看试题解析
6. 如图， $A E ⊥ A B$ 且 $A E = A B ， B C ⊥ C D$ 且 $B C = C D$ ，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）

A、50 B、62 C、65 D、68

查看试题解析
7. 已知x²+2mx+16是完全平方式，则m的值是（　　）

A、±4 B、4 C、﹣4 D、±8

查看试题解析
8. 下列说法错误的是（　　）

A、三角形的中线、高、角平分线都是线段 B、任意三角形内角和都是180° C、三角形按角可分为锐角三角形、直角三角形和等腰三角形 D、直角三角形两锐角互余

查看试题解析

9. 课本中给出了用直尺和圆规作

∠ A O B

的平分线的方法．

作法

图形

①以点O为圆心，任意长为半径作弧，分别交射线 $O A$ 、 $O B$ 于点C、D．②分别以点C、D为圆心，大于 $\frac{1}{2} C D$ 的长为半径作弧，两弧在 $∠ A O B$ 的内部交于点M．

③作射线 $O M$ ．

$O M$ 就是 $∠ A O B$ 的平分线．

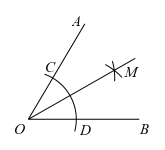
该作图依据是（）

A、

S A S

B、

A A S

C、

A S A

D、

S S S

查看试题解析

10. 如图，CA⊥AB，垂足为点A，AB＝12米，AC＝6米，射线BM⊥AB，垂足为点B，动点E从A点出发以2米/秒沿射线AN运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED＝CB，当点E经过t秒时，由点D、E、B组成的三角形与△BCA全等．请问t有几种情况？（）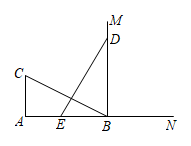

A、1种 B、2种 C、3种 D、4种

查看试题解析

二、填空题（本题有5小题，每小题3分，共15分）

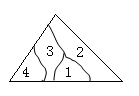
11. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块）你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形?应该带.依据

查看试题解析
12. 蜡烛高 $20 c m$ ，点燃后平均每小时燃掉 $4 c m$ ，则蜡烛点燃后剩余的高度 $h (c m)$ 与燃烧时间 $t ($ 时）之间的关系式是．

查看试题解析
13. 如图，若∠1+∠3=180°，则图中与∠1相等的角有个，与∠1互补的角有个.

查看试题解析
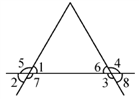14. 任意给定一个非零数，按下列程序计算，最后输出的结果是 $. ($ 最简结果 $)$

查看试题解析
15. 平面镜在光学仪器中有广泛的应用．平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图①，一束光线m射到平面镜a上，被a反射后的光线为n，则 $∠ 1 = ∠ 2$ .如图②，两平面镜 $O M ， O N$ 的夹角 $∠ M O N$ ，若任何射到平面镜 $O N$ 上的入射光线 $A B$ ，经过平面镜 $O N ， O M$ 两次反射后，使得 $A B ∥ C D$ ，则 $∠ M O N =$ °．

查看试题解析

三、解答题（共7题，共55分）

16. 计算：

(1)、 (π-3)⁰+( $\frac{1}{2}$ )^-2+(-1)²⁰²²；

(2)、x·x²·x³+(x²)³-2(x³)²；

(3)、 (a+3b-2c)(a+3b+2c)；

(4)、 2022²-2021×2023．

查看试题解析
17. 先化简，再求值： [(x+2y)²-(x-2y)²-(x+2y)(x-2y)-4y²]÷2x，其中x=-2，y= $\frac{1}{2}$ ；

查看试题解析
18. 完成下面的证明．
如图，已知 $∠ 1 + ∠ B D G = 180 °$ ， $∠ D E F = ∠ B$ ，
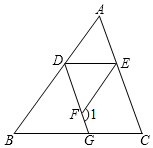
求证： $∠ A E D = ∠ C$
证明： $∵ ∠ 1 + ∠ E F D = 180 ° ($ 邻补角定义 $)$
且 $∠ 1 + ∠ B D G = 180 ° ($ 已知 $)$
$∴ ∠ E F D = ∠ B D G ($ 同角的补角相等 $)$
$∴ A B / / E F ($       $)$
$∴ ∠ D E F = ∠$             ▲            （）
又 $∵ ∠ D E F = ∠ B ($ 已知 $)$
$∴ ∠$             ▲             $= ∠ B ($ 等量代换 $)$
$∴ D E / / B C ($       $)$
$∴ ∠ A E D = ∠ C ($       $)$

查看试题解析
19. 甲、乙两车从 $A$ 城出发匀速行驶至 $B$ 城．在整个行驶过程中，甲、乙两车离开 $A$ 城的距离 $y ($ 千米 $)$ 与甲车行驶的时间 $t ($ 小时 $)$ 之间的函数关系如图所示，则下列结论：

(1)、在上述变化过程中，自变量是，因变量是；

(2)、 $① A$ ， $B$ 两城相距千米；
      $②$ 乙车比甲车晚出发小时， $($ 填甲车或乙车 $)$ 先到达 $B$ 城；
      $③$ 乙车出发后小时追上甲车；
      $④$ 当甲、乙两车相距 $50$ 千米时， $t =$ ．

查看试题解析
20. 如图，在△ABC中，AD是BC边上的高，∠B＝30°，∠ACB＝100°，AE平分∠BAC，求∠EAD的度数.

查看试题解析
21. 【阅读理解】若 $x$ 满足 $(9 - x) (x - 4) = 4$ ，求 ${(9 - x)}^{2} + {(x - 4)}^{2}$ 的值．
解：设 $9 - x = a$ ， $x - 4 = b$ ，则 $(9 - x) (x - 4) = a b = 4$ ， $a + b = (9 - x) + (x - 4) = 5$ ，

$∴ {(9 - x)}^{2} + {(x - 4)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 5^{2} - 2 \times 4 = 17$ ．

这种方法叫做换元法，利用换元法达到简化方程的目的，体现了转化的数学思想．

请仿照上例解决下面的问题：

(1)、若 $x$ 满足 $(50 - x) (x - 20) = 40$ ，求 ${(50 - x)}^{2} + {(x - 20)}^{2}$ 的值．

(2)、若 $x$ 满足 $(8 - x) (2 - x) = 12$ ，求代数式 ${(10 - 2 x)}^{2}$ 的值．

(3)、已知正方形 $A B C D$ 的边长为 $x$ ， $E$ ， $F$ 分别是 $A D$ 、 $D C$ 上的点，且 $A E = 3$ ， $C F = 5$ ，长方形 $E M F D$ 的面积是48，分别以 $M F$ 、 $D F$ 作正方形，求阴影部分的面积．

查看试题解析
22.

(1)、方法学习：数学兴趣小组活动时，张老师提出了如下问题：如图1，在△ABC中，AB＝8，AC＝6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法（如图2），
①延长AD到M，使得DM＝AD；
②连接BM，通过三角形全等把AB、AC、2AD转化在△ABM中；
③利用三角形的三边关系可得AM的取值范围为AB-BM＜AM＜AB+BM，从而得到AD的取值范围是　；

(2)、方法总结：上述方法我们称为“倍长中线法”．“倍长中线法”多用于构造全等三角形和证明边之间的关系．
请你写出图2中AC与BM的数量关系和位置关系，并加以证明．

(3)、深入思考：如图3，AD是△ABC的中线，AB＝AE，AC＝AF，∠BAE＝∠CAF＝90°，请直接利用（2）的结论，试判断线段AD与EF的数量关系，并加以证明．

查看试题解析