浙江省杭州市拱墅区锦绣育才教育集团2024年中考数学一模试卷

试卷更新日期：2024-04-12 类型：中考模拟

进入出卷网下载

一、选择题（本题有10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项最符合题目要求）

1. 把笔尖放在数轴的原点，沿数轴先向左（负方向）移动6个单位长度，再向右移动3个单位长度，用算式表示上述过程与结果，正确的是（）

A、﹣6+3＝9 B、﹣6﹣3＝﹣3 C、﹣6+3＝﹣3 D、﹣6+3＝3

查看试题解析
2. 杭州第19届亚运会开幕式于2023年9月23日晚在杭州奥体中心体育场举行，除现场观众外，最高有110000000人同时在线上参与活动．将数字110000000用科学记数法表示应为（）

A、11×10¹¹ B、1.1×10¹¹ C、1.1×10⁶ D、1.1×10⁸

查看试题解析
3. 如图，AB∥CD，∠A＝60°，则∠1的度数是（）

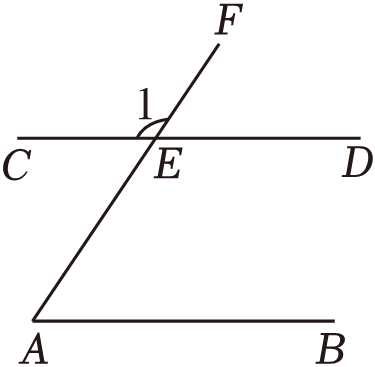A、60° B、90° C、120° D、130°

查看试题解析
4. 王老汉要将一块如图所示的三角形土地平均分配给两个儿子，则图中他所作的线段AD应该是△ABC的（）

A、角平分线 B、中线 C、高线 D、以上都不是

查看试题解析
5. 已知x＜y，则下列不等式一定成立的是（）

A、x+5＜y+1 B、2x+2＜2y+2 C、 $\frac{x}{3} > \frac{y}{3}$ D、﹣2x+5＜﹣2y+5

查看试题解析
6. 已知方程组 ${\begin{array}{l} x + y = 4 \\ y + z = 6 \\ z + x = 8 \end{array}$ ，则 $x + y + z$ 的值是（）

A、9 B、8 C、7 D、6

查看试题解析
7. 小明在平面直角坐标系内画了一个一次函数的图象，图象特点如下：
①图象过点（1，﹣4）②图象与y轴的交点在x轴下方③y随x的增大而减小
符合该图象特点的函数关系式为（）

A、y＝﹣4x+2 B、y＝﹣3x﹣1 C、y＝3x+1 D、y＝﹣5x﹣1

查看试题解析
8. 定义符号min{a，b}的含义为：当a≥b时min{a，b}＝b；当a＜b时min{a，b}＝a．如min{1，﹣3}＝﹣3，min{﹣4，﹣2}＝﹣4．则min（﹣x²+3，﹣2x}的最大值是（）

A、3 B、2 C、1 D、0

查看试题解析
9. 如图，在△ABC中，AB+AC＝ $\frac{5}{3}$ BC，AD⊥BC于D，⊙O为△ABC的内切圆，设⊙O的半径为R，AD的长为h，则 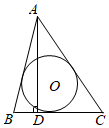$\frac{R}{h}$ 的值为（）

A、 $\frac{3}{8}$ B、 $\frac{2}{7}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
10. 如图，在矩形ABCD中， $A D = 3 A B = 3 \sqrt{10}$ ，点P是AD的中点，点E在BC上，CE＝2BE，点M、N在线段BD上．若△PMN 是等腰三角形且底角与∠DEC相等，则MN的值为（）

A、6或2 B、3或 $\frac{15}{8}$ C、2或3 D、6或 $\frac{15}{8}$

查看试题解析

二、填空题（本题有6个小题，每小题4分，共24分）

11. 计算：﹣10+12＝；|+8|＝．

查看试题解析
12. 从拼音“yucai”的五个字母中随机抽取一个字母，抽中字母u的概率为．

查看试题解析
13. 如图，函数y＝﹣3x和y＝kx+b的图象交于点A（m，4），则关于x的不等式（k+3）x+b＜0的解集为．

查看试题解析
14. 如图，在△ABC 中，已知AB=2，AD⊥BC，垂足为D，BD=2CD．若E是AD的中点，则EC=

查看试题解析
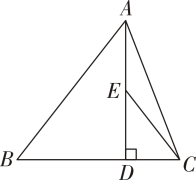15. 一次数学考试共有8道判断题，每道题10分，满分80分．规定正确的画√，错误的画×．甲、乙、丙、丁四名同学的解答及得分情况如表所示，则m的值为．
题号学生
1
2
3
4
5
6
7
8
得分
甲
×
√
×
√
×
×
√
×
60
乙
×
×
√
√
√
×
×
√
50
丙
√
×
×
×
√
√
√
×
50
丁
×
√
×
√
√
×
√
√
m

查看试题解析
16. 在直角坐标系xOy中，对于直线l：y＝kx+b，给出如下定义：若直线l与某个圆相交，则两个交点之间的距离称为直线l关于该圆的“圆截距”．如图，点M的坐标为（﹣1，0），若⊙M的半径为2，当k的取值在实数范围内变化时，直线l关于⊙M的“圆截距”的最小值为 $2 \sqrt{2}$ ，则b的值为．

查看试题解析

三、解答题（本题有8个小题，共66分.解答应写出文字说明、证明过程或演算步内容关注：学数有邻

17. 小敏与小霞两位同学解方程3（x﹣3）＝（x﹣3）²的过程如下框：

小敏：

两边同除以（x﹣3），得

3＝x﹣3，

则x＝6．

小霞：

移项，得3（x﹣3）﹣（x﹣3）²＝0，

提取公因式，得（x﹣3）（3﹣x﹣3）＝0．

则x﹣3＝0或3﹣x﹣3＝0，

解得x₁＝3，x₂＝0．

你认为他们的解法中是否有正确的？如果有，指出哪位同学的解法正确；如果没有，写出正确的解法．

查看试题解析

18. 在学校组织的“学习强国”知识竞赛中，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分和70分．八年级的李老师将801班和802班的成绩进行整理并绘制成如图的统计图．

(1)、在本次竞赛中，802班C级的人数有多少？

(2)、结合如表的统计量：
成绩
班级
平均数（分）
中位数（分）
众数（分）
B级及以上人数
801班
87.6
90
90
18
802班
87.6
80
100
12
请你从不同角度对这次竞赛成绩的结果进行分析（写出两条）．

查看试题解析
19. 关于x的一元二次方程x²﹣6x+k＝0．

(1)、如果方程有两个相等的实数根，求k的值；

(2)、如果x₁ ， x₂是这个方程的两个根，且 $x_{1}^{2}$ + $x_{2}^{2}$ +3x₁•x₂＝25，求k的值．

查看试题解析
20. 已知：如图，∠ADC＝90°，DC∥AB，BA＝BC，AE⊥BC，垂足为点E，点F为AC的中点．

(1)、求证：BF⊥AC；

(2)、求证：△ADC≌△AEC；

(3)、连结DE，若CD＝5，AD＝12，求DE的长．

查看试题解析
21. 学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．

(1)、根据图象信息，求出甲和乙的速度各为多少？（单位：米/分钟）

(2)、求线段AB所在的直线的函数表达式；

(3)、在整个过程中，请通过计算，t为何值时两人相距400米？

查看试题解析
22. 如图，在正方形ABCD中，E是边BC上的一动点（不与点B、C重合），连接DE、点C关于直线DE的对称点为C^' ，连接AC^'并延长交直线DE于点P，F是AC^'的中点，连接DF．

(1)、求∠FDP的度数；

(2)、连接BP，求证： $B P + D P = \sqrt{2} A P$ ；

(3)、连接AC，若正方形的边长为10，求△ACC^'的面积最大值．

查看试题解析
23. 在平面直角坐标系中，抛物线y＝ax²﹣（a+2）x+2经过点A（﹣2，t），B（m，p）．

(1)、若t＝0，
①求此抛物线的对称轴；
②当p＜t时，直接写出m的取值范围；

(2)、若t＜0，点C（n，q）在该抛物线上，m＜n且5m+5n＜﹣13，请比较p，q的大小，并说明理由．

查看试题解析
24. 如图，AB是⊙O的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD＝BD，连接AC交⊙O于点F，连接AE、DE、DF．

(1)、证明：AB＝AC；

(2)、若∠E＝54°，求∠BDF的度数；

(3)、设DE交AB于点G，若DF＝4， $c o s B = \frac{2}{3}$ ， E是 $\overset{⌢}{A B}$ 的中点，求EG•ED的值．

查看试题解析

题号学生	1	2	3	4	5	6	7	8	得分
甲	×	√	×	√	×	×	√	×	60
乙	×	×	√	√	√	×	×	√	50
丙	√	×	×	×	√	√	√	×	50
丁	×	√	×	√	√	×	√	√	m