浙江省金华市东阳市横店四校联考2023-2024学年七年级下学期3月月考数学试题

试卷更新日期：2024-04-12 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 如图， $∠ 1$ 的同位角是（）

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
2. 计算 $x^{3} \cdot x^{3}$ 的结果是（）

A、 $2 x^{3}$ B、 $2 x^{6}$ C、 $x^{6}$ D、 $x^{9}$

查看试题解析
3. 在同一平面内有 $a$ ， $b$ ， $c$ 三条直线，若 $a ∥ b$ ，且 $a$ 与 $c$ 相交，那么 $b$ 与 $c$ 的位置关系是（）

A、平行 B、相交 C、平行或相交 D、不能确定

查看试题解析
4. 已知二元一次方程组 ${\begin{array}{l} x + y = 1 \\ * \end{array}$ 的解是 ${\begin{array}{l} x = - 1 \\ y = a \end{array}$ ，则 $*$ 表示的方程可能是（）

A、 $x - y = - 3$ B、 $x + y = 4$ C、 $2 x - y = - 3$ D、 $2 x + 3 y = - 4$

查看试题解析
5. 如图，点 $E$ 在线段 $B C$ 的延长线上，下列四个结论中正确的个数是（）
①如果 $∠ 3 = ∠ 4$ ，那么 $A D ∥ B C$ ；②如果 $∠ 1 = ∠ 2$ ，那么 $A D ∥ B C$ ；③如果 $A D ∥ B C$ ，那么 $∠ D + ∠ B C D = 180 °$ ；④如果 $A B ∥ D C$ ，那么 $∠ B = ∠ 5$

A、1 B、2 C、3 D、4

查看试题解析
6. 李明一家自驾旅行，车上备了一些矿泉水，如果每人分2瓶，则多出4瓶，如果每人分3瓶，则有一人少一瓶．设这一行人共有 $x$ 人，矿泉水一共 $y$ 瓶，下列方程组中正确的是（）

A、 ${\begin{array}{l} 2 x + 4 = y \\ 3 x + 1 = y \end{array}$ B、 ${\begin{array}{l} 2 x + 4 = y \\ 3 x - 1 = y \end{array}$ C、 ${\begin{array}{l} 2 x - 4 = y \\ 3 x + 1 = y \end{array}$ D、 ${\begin{array}{l} 2 x - 4 = y \\ 3 x - 1 = y \end{array}$

查看试题解析
7. 如图1，数学课上，老师在黑板上画出两条直线 $a$ ， $b$ ，两条直线所成的角跑到黑板外面去了，老师让小明在黑板上测量出直线 $a$ ， $b$ 所成的角的度数，小明在图 2 中画出测量示意图，过直线 $b$ 上一点 $P$ ，作 $c ∥ a$ ．测量 $b$ 与 $c$ 的夹角 $∠ 1$ 就是 $a$ 、 $b$ 所成的角的度数．这种画图方法的数学依据是（）．

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
8. 若 $∠ α$ 与 $∠ β$ 的两边分别平行，且 $∠ α = (3 m - 10) °$ ， $∠ β = (m + 30) °$ ，则 $∠ α$ 的度数为（）

A、 $50 °$ B、 $110 °$ C、 $50 °$ 或 $110 °$ D、 $20 °$ 或 $40 °$

查看试题解析
9. 已知关于x，y的方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是 ${\begin{array}{l} x = 2.1 \\ y = 4.5 \end{array}$ .则关于x，y的方程组 ${\begin{array}{l} a_{1} (x - 2) + 3 b_{1} y = 2 c_{1} \\ a_{2} (x - 2) + 3 b_{2} y = 2 c_{2} \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 4.1 \\ y = 13.5 \end{array}$ B、 ${\begin{array}{l} x = 4.2 \\ y = 4.5 \end{array}$ C、 ${\begin{array}{l} x = 6.2 \\ y = 9 \end{array}$ D、 ${\begin{array}{l} x = 6.2 \\ y = 3 \end{array}$

查看试题解析
10. 如图，将长方形纸片 $A B C D$ 沿 $E F$ 折叠后，点 $A$ ， $B$ 分别落位 $A^{'}$ ， $B^{'}$ 的位置．再将 $△ A^{'} E G$ 沿 $A D$ 翻折得到 $△ H E G$ ， ①若 $H G ∥ F B^{'}$ ，则 $∠ 1 = 4 5^{∘}$ ． ②若点 $H$ 恰好落在线段 $E F$ 上．则 $∠ 1 = 6 0^{∘}$ ．关于上述两个结论说法正确的是（）

A、①正确，②错误 B、①错误，②正确 C、①②都正确 D、①②都错误

查看试题解析

二、填空题（每小题4分，共24分）

11. 已知 $2 x - 3 y = 6$ ，用含 $x$ 的代数式表示 $y$ ，则 $y =$ .

查看试题解析
12. 如图，△ABC沿AB方向向右平移后得到△DEF，若CF=5cm，BD=3cm，则AE=.

查看试题解析
13. 如图，直线 $a$ ， $b$ 被直线 $c$ 所截， $∠ 1 = 10 2^{∘}$ ，若要使 $a ∥ b$ ，则 $∠ 2 =$ ．

查看试题解析
14. 对于 $x$ ， $y$ 定义一种新运算 $x * y = a x + b y - 1$ （ $a$ ， $b$ 是非零常数）．例如 $0 * 0 = a \times 0 + b \times 0 - 1 = - 1$ ．若 $1 * 2 = 3$ ， $2 * (- 1) = 0$ ，则 $a =$ ， $b =$ ．

查看试题解析
15. 图1，由两个相同的小长方形组成的图形周长为10，图2中在长方形ABCD内放置了若干个相同的小长方形，则长方形ABCD的周长为.

查看试题解析
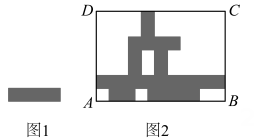16. 图1 是一盏可折叠台灯，图 2，图 3 是其平面示意图，固定底座 $O A ⊥ O M$ 于点 $O$ ，支架 $B A$ 与 $C B$ 分别可绕点 $A$ 和 $B$ 旋转，台灯灯罩且可绕点 $C$ 旋转调节光线角度，台灯最外侧光线 $C E$ ， $C D$ 组成的 $∠ E C D$ 始终保持不变．如图2，调节台灯使光线 $C D ∥ B A$ ， $C E ∥ O M$ ，此时 $∠ B A O = 158 °$ ，则 $∠ E C D =$ ．现继续调节图2中的支架 $C B$ 与灯罩，发现当最外侧光线 $C E$ 与水平方向的夹角 $∠ C Q M = 29 °$ ，且 $∠ E C D$ 的角平分线 $C P$ 与 $C B$ 垂直时，光线最适合阅读（如图3），则此时 $∠ A B C =$ ．

查看试题解析

三、解答题（共66分）

17. 解方程组：

(1)、 ${\begin{array}{l} 2 x + 3 y = 9 \\ x = 2 y + 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x + 2 y = 4 \\ \frac{3 x}{2} - \frac{y + 1}{3} = 1 \end{array}$ ．

查看试题解析
18. 如图，在正方形网格中，每个小正方形的边长均为1个单位长度， $△ A B C$ 的三个顶点都在格点上，点 $M$ 也在格点上．用无刻度的直尺在网格内按要求完成作图并回答问题：

(1)、过点 $M$ 作一条线段 $M N$ 平行且等于 $B C$ ．

(2)、将图中三角形 $A B C$ 先向左平移2个单位，再向上平移2个单位得到三角形 $A^{'} B^{'} C^{'}$ ，
①在图中作出平移后的三角形 $A^{'} B^{'} C^{'}$ ．
②在平移过程中，线段 $A B$ 扫过的面积为 ▲ ．

查看试题解析
19. 甲、乙两名同学在解方程组 ${\begin{array}{l} a x - y = 13 \\ x - b y = 4 \end{array}$ 时，甲同学因看错了 $a$ ，从而求得解为 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，乙同学因看错了 $b$ ，从而求得解为 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ ，计算 $a^{6} \cdot b^{3}$ ，并用幂的形式表示结果．

查看试题解析
20. 如图，已知 $∠ 1 + ∠ 2 = 180 °$ ，且 $E F ∥ B C$ ．

(1)、判断 $∠ 3$ 与 $∠ C$ 的数量关系，并说明理由；

(2)、若 $E F$ 平分 $∠ A F D$ ， $∠ C = 34 °$ ，求 $∠ A B C$ 的度数．

查看试题解析
21. 已知关于x，y的方程组 ${\begin{array}{l} 2 x + y = a \\ 3 x + 2 y = 3 a - 1 \end{array}$ .

(1)、若方程组的解满足 $x + y = 0$ ，求 $a$ 的值；

(2)、当 $a$ 取不同实数时， $x + \frac{1}{3} y$ 的值是否发生变化，如果不变，求出 $x + \frac{1}{3} y$ 的值，如果改变，请说明理由。

(3)、x，y的自然数解是.

查看试题解析
22. 如图

(1)、阅读并补全上述推理过程．
如图1，已知点 $A$ 在 $B C$ 外一点，连接 $A B$ ， $A C$ ．求 $∠ B A C + ∠ B + ∠ C$ 的度数．
解：过点 $A$ 作 $E D ∥ B C$ ，
$∴ ∠ B =$ ▲ ， $∠ C =$ ▲ ．（）
又 $∵ ∠ E A B + ∠ B A C + ∠ D A C = 180 °$ ．
$∴ ∠ B + ∠ B A C + ∠ C =$ ▲ ．
从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将 $∠ B A C$ ， $∠ B$ ， $∠ C$ “凑”在一起，得出角之间的关系，使问题得以解决．

(2)、如图2所示，已知 $A B ∥ C D$ ， $B E$ 、 $C E$ 交于点 $E$ ， $∠ B E C = 85 °$ ，在图2的情况下求 $∠ B - ∠ C$ 的度数．

(3)、如图3，已知 $A B ∥ C D$ ， $B E$ 、 $C E$ 交于点 $E$ ， $B F$ 、 $C G$ 分别平分 $∠ A B E$ 、 $∠ E C D$ ，直线 $B F$ 与直线 $C G$ 交于点 $F$ ，若 $∠ F = 42 °$ ，则 $∠ B E C =$ ．

查看试题解析
23. 塘栖枇杷是余杭的特色产品，肉质细嫩、汁多味鲜，塘栖枇杷有着非常悠久的历史，据相关文献记载，塘栖枇杷的种植距今已经有 1400多年的历史．某销售商将 $255 k g$ 塘栖枇杷分成 $A$ 型、 $B$ 型两种礼盒进行销售，① $A$ 型每盒 $2 k g$ ，每盒售价 $a$ 元；② $B$ 型每盒 $3.5 k g$ ，每盒售价比 $A$ 型价格的2倍少50元．某位顾客买了一盒 $A$ 型，两盒 $B$ 型，一共花费340 元．

(1)、请问 $A$ 型、 $B$ 型售价分别是多少元？

(2)、假设用这两种包装方式恰好包装完所有的枇杷．销售总收入为9820元．
①若这批塘栖枇杷全部售完，请问 $A$ 型、 $B$ 型分别有多少盒？
②若该销售商留下 $m (m > 0)$ 盒 $A$ 型礼盒送人，剩余礼盒全部售出，求出 $m$ 的值．

查看试题解析
24. 如图，已知射线 $A Q ∥$ 直线 $D N$ ，点 $B$ 、 $C$ 分别是射线 $A Q$ 、射线 $D N$ 上的动点， $∠ A B C = ∠ A D C = 100 °$ ．

(1)、直线 $A D$ 与 $B C$ 有何位置关系？请说明理由；

(2)、若点 $E$ 在直线 $D N$ 上，且满足 $∠ C A B = ∠ E A C$ ， $A F$ 平分 $∠ D A E$ 交直线 $D N$ 于点 $F$ ．
①当 $B$ 、 $C$ 运动时， $\frac{∠ F A C}{∠ D A B} =$ ▲ ．
②若 $∠ D F A - ∠ D A F = 44 °$ ，求 $∠ A C B$ 的度数．
③若 $∠ A F D = ∠ A C B$ ， $△ A C F$ 绕点 $A$ 逆时针旋转，旋转角为 $β (0 ° < β \leq 180 °)$ ，则在旋转过程中， $△ A C F$ 的边 $C F$ 与 $△ A D F$ 的某一边平行时，直接写出此时 $β$ 的值．

查看试题解析