浙江省温州市2024年中考一模数学试题
试卷更新日期:2024-04-12 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各数中立方根为的是( )A、1 B、 C、 D、3. 如图是由六个相同的小正方体搭成的几何体,这个几何体的左视图是( )
2. 下列各数中立方根为的是( )A、1 B、 C、 D、3. 如图是由六个相同的小正方体搭成的几何体,这个几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列调查所采用的调查方式,不合适的是( )A、了解楠溪江的水质,采用抽样调查 B、了解浙江省中学生的睡眠时间,采用抽样调查 C、检测祝融号火星探测器的零部件质量,采用抽样调查 D、了解某校初三段数学老师的视力,采用全面调查5. 四个实数 , 6, , 中,最大的无理数是( )A、 B、6 C、 D、6. 若点 , , 在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,等边的顶点 , , 已知与位似,位似中心是原点O,且的面积是面积的16倍,则点A对应点的坐标为( )
4. 下列调查所采用的调查方式,不合适的是( )A、了解楠溪江的水质,采用抽样调查 B、了解浙江省中学生的睡眠时间,采用抽样调查 C、检测祝融号火星探测器的零部件质量,采用抽样调查 D、了解某校初三段数学老师的视力,采用全面调查5. 四个实数 , 6, , 中,最大的无理数是( )A、 B、6 C、 D、6. 若点 , , 在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,等边的顶点 , , 已知与位似,位似中心是原点O,且的面积是面积的16倍,则点A对应点的坐标为( )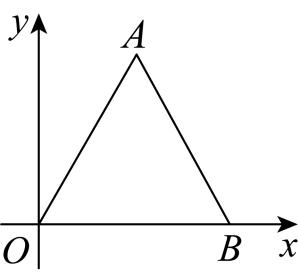 A、 B、或 C、 D、或8. 如图,在矩形中,点为的中点,将沿所在直线翻折压平,得到 , 延长与交于点 , 若 , , 则四边形的面积为( )
A、 B、或 C、 D、或8. 如图,在矩形中,点为的中点,将沿所在直线翻折压平,得到 , 延长与交于点 , 若 , , 则四边形的面积为( ) A、 B、 C、 D、9. 如图,网格小正方形边长为3,的三个顶点均在网格的格点上,中线的交点为O,则的长度为( )
A、 B、 C、 D、9. 如图,网格小正方形边长为3,的三个顶点均在网格的格点上,中线的交点为O,则的长度为( )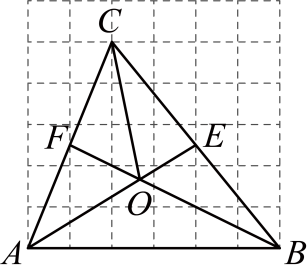 A、 B、 C、 D、10. 如图,已知函数图象与x轴只有三个交点,分别是 , , .
A、 B、 C、 D、10. 如图,已知函数图象与x轴只有三个交点,分别是 , , .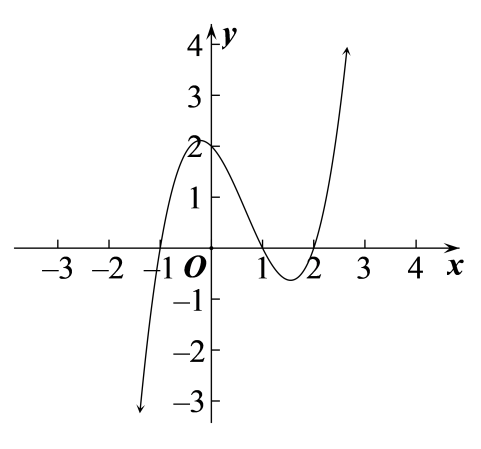
①当时,或;②当时,y有最小值,没有最大值;③当时,y随x的增大而增大;④若点在函数图象上,则m的值只有3个.上述四个结论中正确的有( )
A、①② B、①②④ C、①③④ D、②③④二、填空题(本题有6小题,每小题4分,共24分)
-
11. 关于的不等式的解是 .12. 已知 , , 则多项式的值为 .13. 若半径为的扇形弧长为 , 则该扇形的圆心角度数为 .14. 如图,的内接四边形 , , 的直径与交于点F,连接 . 若 , , , 则的长为 .
 15. 第二十四届国际数学家大会会微的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形和中间一个小正方形拼成的大正方形中,连接 . 若的内切圆半径为1,小正方形的面积为16,则大正方形的面积为 .
15. 第二十四届国际数学家大会会微的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形和中间一个小正方形拼成的大正方形中,连接 . 若的内切圆半径为1,小正方形的面积为16,则大正方形的面积为 . 16. 已知 , 为x轴上两点, , 为二次函数图象上两点,当时,二次函数y随x增大而减小,若 , 时,恒成立,则A、B两点的最大距离为 .
16. 已知 , 为x轴上两点, , 为二次函数图象上两点,当时,二次函数y随x增大而减小,若 , 时,恒成立,则A、B两点的最大距离为 .三、解答题(本题有8小题,共66分)
-
17. 计算:(1)、(2)、18. 如图的网格中,的顶点都在格点上,每个小正方形的边长均为1.仅用无刻度的直尺在给定的网格图中分别按下列要求画图.(保留画图痕迹,画图过程中辅助线用虚线,画图结果用实线、实心点表示)
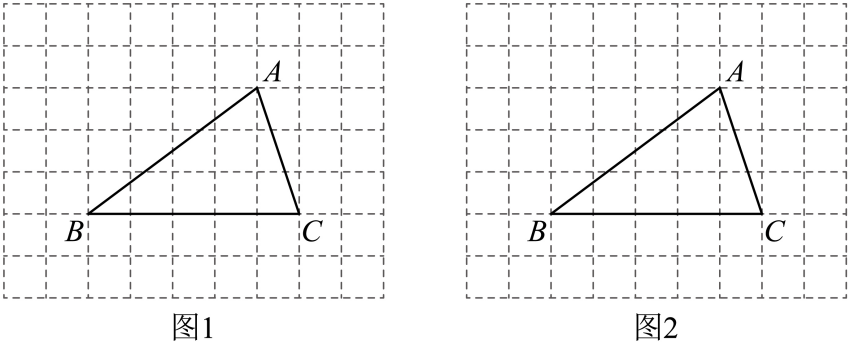 (1)、请在图1中画出的高 .(2)、请在图2中在线段上找一点E,使 .19. 如图,在菱形中, , , 为正三角形,点E,F分别在菱形的边 . 上滑动,且点E、F不与点A,B,C重合,与交于点G.
(1)、请在图1中画出的高 .(2)、请在图2中在线段上找一点E,使 .19. 如图,在菱形中, , , 为正三角形,点E,F分别在菱形的边 . 上滑动,且点E、F不与点A,B,C重合,与交于点G.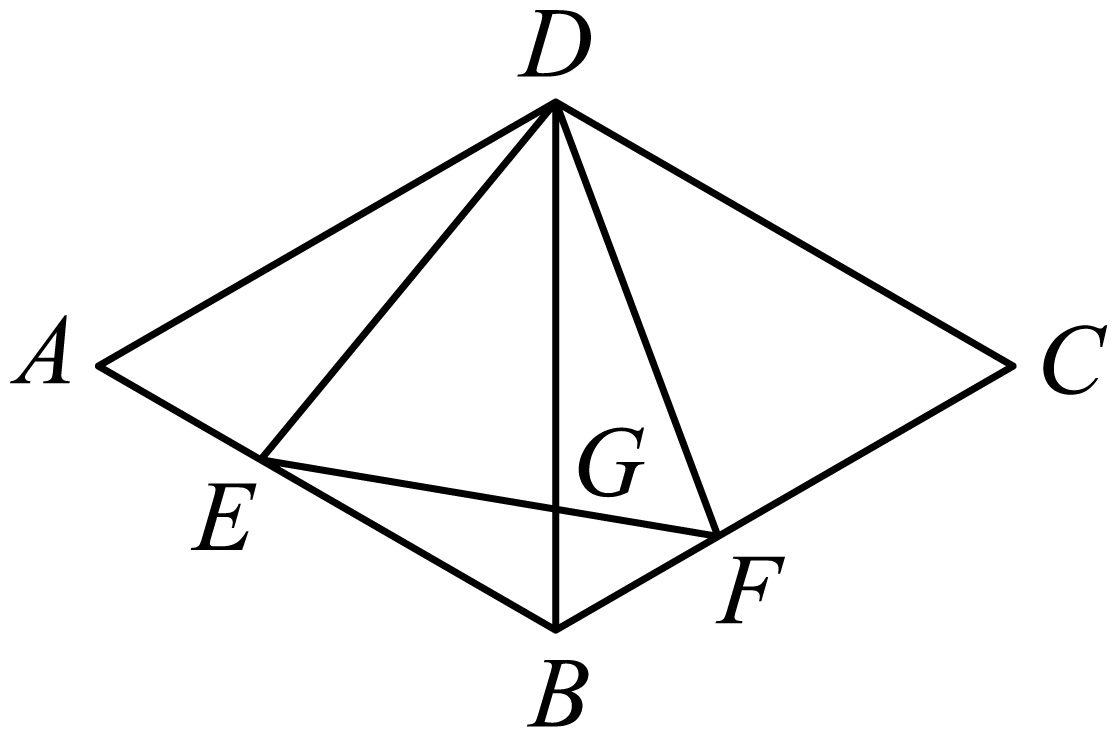 (1)、证明:当点E,F在边上滑动时,总有 .(2)、当时,求的长.20. 为了了解九年级学生体育训练情况,随机抽取男生、女生各名进行分钟跳绳测试,并对测试结果进行整理,分钟跳绳的个数用表示,分成了四个等级,其中: , : , : , : , 下面给出了部分统计信息:
(1)、证明:当点E,F在边上滑动时,总有 .(2)、当时,求的长.20. 为了了解九年级学生体育训练情况,随机抽取男生、女生各名进行分钟跳绳测试,并对测试结果进行整理,分钟跳绳的个数用表示,分成了四个等级,其中: , : , : , : , 下面给出了部分统计信息:信息一:女生分钟跳绳个数等级扇形统计图
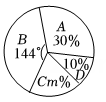
信息二:男生分钟跳绳个数等级频数统计表
等级
频数
信息三:男生和女生分钟跳绳个数的平均数,众数,中位数,等级所占百分比如下表:
平均数
众数
中位数
A等级所占百分比
男生
女姓
根据以上信息,解答下列问题:
(1)、 , .(2)、根据以上数据分析,你认为九年级分钟跳绳男生成绩更优异,还是女生成绩更优异?请说明理由(写出一条理由即可)(3)、在跳绳个数达到等级的同学中有两名男生和一名女生跳绳的个数超过了个,体育老师随机从这三位同学中选择两位同学做经验分享,请利用画树状图或列表的方法,求选到这名女生的概率是多少?21. “字母表示数”的系统化阐述是16世纪提出的,被后人称为从“算术”到“代数”的一次飞跃,从而大大推动了数学的发展.经过初中数学的学习,我们知道了用字母表示数可以分析从特殊到一般的数学规律,字母与数一样,也可以参与运算.请同学们观察下列关于正整数的平方拆分的等式:第1个等式:;第2个等式:;
第3个等式:;第4个等式:;
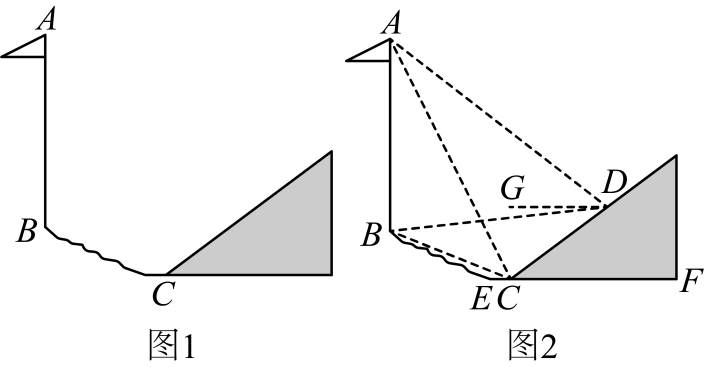
(1)、请用此方法拆分 .(2)、请你用上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数)并运用有关知识,推理说明这个结论是正确的.22. 已知二次函数 .(1)、若它的图象经过点 , 求该函数的对称轴.(2)、若时,y的最小值为1,求出t的值.(3)、如果 , 两点都在这个二次函数的图象上,直线与该二次函数交于 , 两点,则是否为定值?若是,请求出该定值:若不是,请说明理由.23. 【问题背景】一旗杆直立(与水平线垂直)在不平坦的地面上(如图1).两个学习小组为了测量旗杆的高度,准备利用附近的小山坡进行测量估算.
 (1)、【问题探究】
(1)、【问题探究】如图2,在坡角点C处测得旗杆顶点A的仰角的正切值为2,山坡上点D处测得顶点A的仰角的正切值为 , 斜坡的坡比为 , 两观测点的距离为 .
学习小组成员对问题进行如下分解,请探索并完成任务.
①计算C,D两点的垂直高度差.
②求顶点A到水平地面的垂直高度.
(2)、【问题解决】为了计算得到旗杆的高度,两个小组在共同解决任务1和2后,采取了不同的方案:
小组一:在坡角点C处测得旗杆底部点B的仰角的正切值为;
小组二:在山坡上点D处测得旗杆底部点B的俯角的正切值为 .
请选择其中一个小组的方案计算旗杆的高度.
24. 如图1,锐角内接于 , 点E是的中点,连结并延长交于D,点F在上,连结 , , .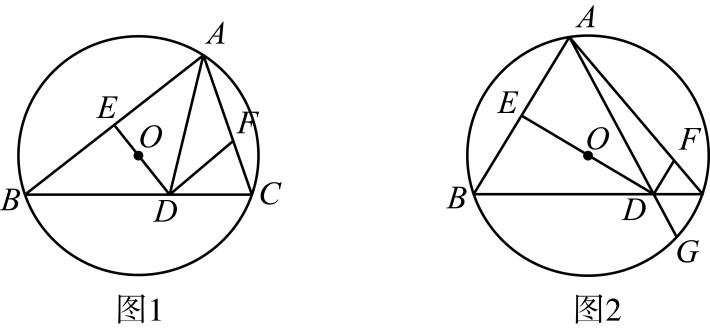 (1)、求证: .(2)、当 , 时,
(1)、求证: .(2)、当 , 时,①求的值;
②求的长.
(3)、如图2,延长AD交于点G,若 , 求的值.