浙江省台州市2024年中考一模数学试卷
试卷更新日期:2024-04-12 类型:中考模拟
一、选择题(本题共10小题,每小题3分,共30分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
-
1. 下列是几个城市地铁标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列能使有意义的是( )A、x=-5 B、x=-3 C、x=1 D、x=33. 下列运算正确的是( )A、a2•a3=a5 B、(a2)4=a6 C、a8÷a2=a4 D、a5+a5=2a104. 一个多边形的内角和为720°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形5. 下列收集数据的方式合理的是( )A、为了解残疾人生活、就业等情况,在某网站设置调查问卷 B、为了解一个省的空气质量,调查了该省省会城市的空气质量 C、为了解某校学生视力情况,抽取该校各班学号为5的整数倍的同学进行调查 D、为了解某校学生每天的平均睡眠时间,对该校学生周末的睡眠时间进行调查6. 如图,若∠1=∠2=75°,∠3=108°,则∠4的度数是( )
2. 下列能使有意义的是( )A、x=-5 B、x=-3 C、x=1 D、x=33. 下列运算正确的是( )A、a2•a3=a5 B、(a2)4=a6 C、a8÷a2=a4 D、a5+a5=2a104. 一个多边形的内角和为720°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形5. 下列收集数据的方式合理的是( )A、为了解残疾人生活、就业等情况,在某网站设置调查问卷 B、为了解一个省的空气质量,调查了该省省会城市的空气质量 C、为了解某校学生视力情况,抽取该校各班学号为5的整数倍的同学进行调查 D、为了解某校学生每天的平均睡眠时间,对该校学生周末的睡眠时间进行调查6. 如图,若∠1=∠2=75°,∠3=108°,则∠4的度数是( )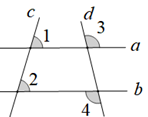 A、75° B、102° C、105° D、108°7. 一辆出租车从甲地到乙地,当平均速度为v(km/h)时,所用时间为t(h),则t关于v的函数图象大致是( )A、
A、75° B、102° C、105° D、108°7. 一辆出租车从甲地到乙地,当平均速度为v(km/h)时,所用时间为t(h),则t关于v的函数图象大致是( )A、 B、
B、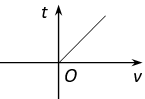 C、
C、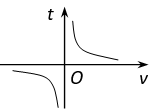 D、
D、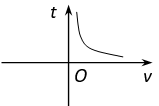 8. 如图,数轴上三个不同的点A,B,P分别表示实数a,b,a+b,则下列关于数轴原点位置的描述正确的是( )
8. 如图,数轴上三个不同的点A,B,P分别表示实数a,b,a+b,则下列关于数轴原点位置的描述正确的是( ) A、原点在点A的左侧 B、原点在A,B两点之间 C、原点在B,P两点之间 D、原点在点P的右侧9. 某省居民生活用电实施阶梯电价,年用电量分为三个阶梯.阶梯电费计价方式如下:
A、原点在点A的左侧 B、原点在A,B两点之间 C、原点在B,P两点之间 D、原点在点P的右侧9. 某省居民生活用电实施阶梯电价,年用电量分为三个阶梯.阶梯电费计价方式如下:阶梯档次
年用电量
电价(单位:元/度)
第一阶梯
2760度及以下部分
0.538
第二阶梯
2761度至4800度部分
0.588
第三阶梯
4801度及以上部分
0.838
小聪家去年12月份用电量为500度,电费为319元,则小聪家去年全年用电量为( )
A、5250度 B、5100度 C、4900度 D、4850度10. 如图,在矩形ABCD中,BC>AB,先以点A为圆心,AB长为半径画弧交边AD于点E;再以点D为圆心,DE长为半径画弧交边DC于点F;最后以点C为圆心,CF长为半径画弧交边BC于点G.求BG的长,只需要知道( )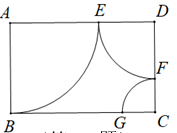 A、线段AB的长 B、线段AD的长 C、线段DE的长 D、线段CF的长
A、线段AB的长 B、线段AD的长 C、线段DE的长 D、线段CF的长二、填空题(本题共6小题,每小题4分,共24分)
-
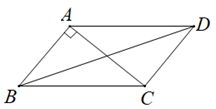
11. 写出一个大于1且小于3的无理数:.12. 因式分解:x2-2xy=.13. 从1至9这些自然数中任意抽取一个数,抽取到的数字能被3整除的概率是.14. 如图,在□ABCD中,AB=3 cm,BC=5 cm,AB⊥AC,则BD的长度为cm.
 15. 如图,△ABC是等腰三角形,AB=AC,∠A=42°,将△BCD沿直线BD翻折,点C的对应点C´恰好落在边AB上,则∠ADC´的度数为.
15. 如图,△ABC是等腰三角形,AB=AC,∠A=42°,将△BCD沿直线BD翻折,点C的对应点C´恰好落在边AB上,则∠ADC´的度数为.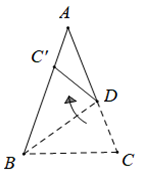 16. 一组有序排列的数具有如下规律:任意相邻的三个数,中间的数等于前后两数的积.若这组数第1个数是a,第5个数是 , 则第2028个数是(用含a的式子表示).
16. 一组有序排列的数具有如下规律:任意相邻的三个数,中间的数等于前后两数的积.若这组数第1个数是a,第5个数是 , 则第2028个数是(用含a的式子表示).三、解答题(本题共8小题,第17~19题每小题6分,第20,21题每小题8分,第22,23题每小题10分,第24题12分,共66分)
-
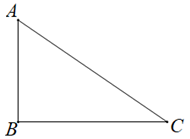
17.(1)、计算:.(2)、解不等式组:18. 尺规作图:如图,请用圆规和无刻度的直尺作出Rt△ABC中斜边AC上的中线BO.(保留作图痕迹,不要求写作法)
 19. 光从空气射入液体会发生折射现象. 如图,水平放置的容器中装有某种液体,光线AO斜射到液面发生折射,折射光线为OB,折射角为∠BOD,测得∠BOD=20°,OD⊥BD,OD=10 cm,求折射光线OB的长.(结果精确到0.1 cm.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36.)
19. 光从空气射入液体会发生折射现象. 如图,水平放置的容器中装有某种液体,光线AO斜射到液面发生折射,折射光线为OB,折射角为∠BOD,测得∠BOD=20°,OD⊥BD,OD=10 cm,求折射光线OB的长.(结果精确到0.1 cm.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36.)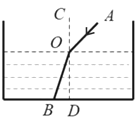 20. 下图是某市轻轨列车两站之间行驶速度v(米/秒)与行驶时间t(秒)之间的函数图象,已知点A(90,40),点B(230,40),点C(270,0).
20. 下图是某市轻轨列车两站之间行驶速度v(米/秒)与行驶时间t(秒)之间的函数图象,已知点A(90,40),点B(230,40),点C(270,0).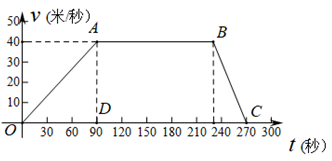 (1)、求线段BC的函数解析式.(2)、求这两站之间列车速度不低于30米/秒的行驶时间.21. 如图,在正方形ABCD中,以BC为边在正方形内部作等边△BCE,CE与正方形的对角线BD交于点F,连接DE.
(1)、求线段BC的函数解析式.(2)、求这两站之间列车速度不低于30米/秒的行驶时间.21. 如图,在正方形ABCD中,以BC为边在正方形内部作等边△BCE,CE与正方形的对角线BD交于点F,连接DE.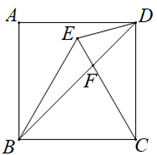 (1)、求∠DEC的度数.(2)、求证:DE2=EF·EC.22. 某饲料生产厂家为了比较1号、2号两种鱼饲料的喂养效果,选出重量基本相同的某种鱼苗360条放养到A,B两个水池,其中A水池200条,B水池160条.在养殖环境、喂料方式等都大致相同的条件下,A水池的鱼用1号饲料喂养,B水池的鱼用2号饲料喂养.假设放养的鱼苗全部成活,且总条数不变,经过12个月后,在A水池、B水池中各随机抽取10条鱼分别进行称重,得到A水池鱼的重量数据(单位:kg):4.5,3.8,3.7,5.3,3.6,3.7,4.9,4.5,3.7,3.6;B水池鱼的重量数据(单位:kg):3.6,3.5,4.4,3.7,3.9,3.4,4.5,3.6,3.3,3.2.(1)、你认为1号、2号饲料哪种喂养效果好?请说明理由.(2)、若要求鱼的重量超过4.0 kg才可以出售,估计此时这360条鱼中符合出售标准的鱼
(1)、求∠DEC的度数.(2)、求证:DE2=EF·EC.22. 某饲料生产厂家为了比较1号、2号两种鱼饲料的喂养效果,选出重量基本相同的某种鱼苗360条放养到A,B两个水池,其中A水池200条,B水池160条.在养殖环境、喂料方式等都大致相同的条件下,A水池的鱼用1号饲料喂养,B水池的鱼用2号饲料喂养.假设放养的鱼苗全部成活,且总条数不变,经过12个月后,在A水池、B水池中各随机抽取10条鱼分别进行称重,得到A水池鱼的重量数据(单位:kg):4.5,3.8,3.7,5.3,3.6,3.7,4.9,4.5,3.7,3.6;B水池鱼的重量数据(单位:kg):3.6,3.5,4.4,3.7,3.9,3.4,4.5,3.6,3.3,3.2.(1)、你认为1号、2号饲料哪种喂养效果好?请说明理由.(2)、若要求鱼的重量超过4.0 kg才可以出售,估计此时这360条鱼中符合出售标准的鱼大约有多少条?
23. 图1是即将建造的“碗形”景观池的模拟图,设计师将它的外轮廓设计成如图2所示的图形.它是由线段AC,线段BD,曲线AB,曲线CD围成的封闭图形,且AC//BD,BD在x轴上,曲线AB与曲线CD关于y轴对称.已知曲线CD是以C为顶点的抛物线的一部分,其函数解析式为:(p 为常数,8≤p≤40).
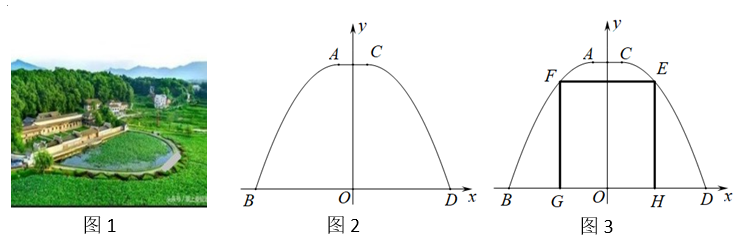 (1)、当p=10时,求曲线AB的函数解析式.(2)、如图3,用三段塑料管EF,FG,EH围成一个一边靠岸的矩形荷花种植区,E,F分别在曲线CD,曲线AB上,G,H在x轴上.
(1)、当p=10时,求曲线AB的函数解析式.(2)、如图3,用三段塑料管EF,FG,EH围成一个一边靠岸的矩形荷花种植区,E,F分别在曲线CD,曲线AB上,G,H在x轴上.①记EF=70米时所需的塑料管总长度为L1 , EF=60米时所需的塑料管总长度为L2.若L1<L2 , 求p的取值范围.
②当EF与AC的差为多少时,三段塑料管总长度最大?请你求出三段塑料管总长度的最大值.
24. 【概念呈现】在钝角三角形中,钝角的度数恰好是其中一个锐角的度数与90度的和,则称这个钝角三角形为和美三角形,这个锐角叫做和美角. (1)、【概念理解】当和美三角形是等腰三角形时,求和美角的度数.(2)、【性质探究】如图1,△ABC是和美三角形,∠B是钝角,∠A是和美角,
(1)、【概念理解】当和美三角形是等腰三角形时,求和美角的度数.(2)、【性质探究】如图1,△ABC是和美三角形,∠B是钝角,∠A是和美角,求证:.
(3)、【拓展应用】如图2,AB是⊙O的直径,且AB=13,点C,D是圆上的两点,弦CD与AB交于点E,连接AD,BD,△ACE是和美三角形.①当BC=5时,求AD的长.
②当△BCD是和美三角形时,直接写出的值.