浙江省宁波市镇海区蛟川书院2024年中考数学一模试卷（3月份）

试卷更新日期：2024-04-12 类型：中考模拟

进入出卷网下载

一、选择题

1. 在Rt△ABC中，∠C＝90°，sinA＝ $\frac{4}{5}$ ，则tanA=（）

A、 $\frac{5}{3}$ B、 $\frac{4}{3}$ C、 $\frac{4}{5}$ D、 $\frac{3}{4}$

查看试题解析
2. 一圆的半径为3，圆心到直线的距离为4，则该直线与圆的位置关系是（）

A、相切 B、相交 C、相离 D、以上都不对

查看试题解析
3. 2015年中国高端装备制造业销售收入将超6万亿元，其中6万亿元用科学记数法可表示为（　　）

A、0.6×10¹³元 B、60×10¹¹元 C、6×10¹²元 D、6×10¹³元

查看试题解析
4. 如图是由五个相同的小立方块搭成的几何体，则它的俯视图是（）

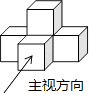A、 B、 C、 D、

查看试题解析
5. 某班10名学生的校服尺寸与对应人数如表所示：
尺寸（cm）
160
165
170
175
180
学生人数（人）
1
3
2
2
2
则这10名学生校服尺寸的众数和中位数分别为（）

A、165cm ， 165cm B、170cm ， 165cm C、165cm ， 170cm D、170cm ， 170cm

查看试题解析
6. 能说明命题“对于任何实数a ， |a|＞﹣a”是假命题的一个反例可以是（）

A、a＝1 B、a＝ $\sqrt{2}$ C、a＝ $\frac{1}{3}$ D、a＝﹣2

查看试题解析
7. 如图，用一个半径为30cm，面积为300πcm²的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为（）

A、5cm B、10cm C、20cm D、5πcm

查看试题解析
8. 如图，在⊙O中，E是直径AB延长线上一点，CE切⊙O于点E，若CE=2BE，则∠E的余弦值为（　　）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
9. 如图，△ABC和△CDE都是等边三角形，点G在CA的延长线上，GB=GE，若BE+CG=10， $\frac{A G}{B E}$ ＝ $\frac{3}{2}$ ，则AF的长为（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{9}{5}$ D、2

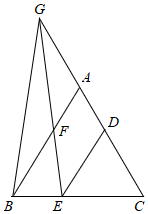查看试题解析
10. 已知二次函数y＝a（x+m﹣1）（x﹣m）（a≠0）的图象上有两点A（x₁ ， y₁）和B（x₂ ， y₂）（其中x₁＜x₂），则（）

A、若a＞0，当x₁+x₂＜1时，a（y₁﹣y₂）＜0 B、若a＞0，当x₁+x₂＜1时，a（y₁﹣y₂）＞0 C、若a＜0，当x₁+x₂＞﹣1时，a（y₁﹣y₂）＜0 D、若a＜0，当x₁+x₂＞﹣1时，a（y₁﹣y₂）＞0

查看试题解析

二、填空题

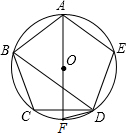
11. 二次根式 $\sqrt{2 x + 1}$ 有意义的条件是．

查看试题解析
12. 袋中装有除颜色外其余均相同的5个红球和3个白球.从袋中任意摸出一个球，则摸出的球是红球的概率为.

查看试题解析
13. 如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，则∠BDF的度数是°．

查看试题解析
14. 一个正三棱柱的三视图如图所示，若这个正三棱柱的表面积为24+8 $\sqrt{3}$ ，则a的值是．

查看试题解析
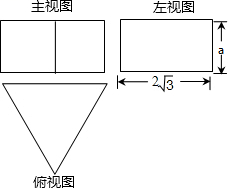15. 已知点（3，m），（5，n）在抛物线y=ax²+bx（a，b为实数，a＜0）上，设抛物线的对称轴为直线x=t，若n＜0＜m，则t的取值范围为．

查看试题解析
16. 如图，在等边三角形ABC中，点D，E分别是边BC，CA上的点，且BD=CE，连结AD，BE交于点P．连接CP，若CP⊥AP时，则AE：CE= ；设△ABC的面积为S₁ ，四边形CDPE的面积为S₂ ，则 $\frac{S_{2}}{S_{1}}$ ＝．

查看试题解析

三、解答题

17.

(1)、计算：（a+1）²+a（2﹣a）．

(2)、解不等式：3x﹣5＜2（2+3x）．

查看试题解析
18. 某学校开展了防疫知识的宣传教育活动．为了解这次活动的效果，学校从全校1500名学生中随机抽取部分学生进行知识测试（测试满分100分，得分x均为不小于60的整数），并将测试成绩分为四个等级：基本合格（60≤x＜70），合格（70≤x＜80），良好（80≤x＜90），优秀（90≤x≤100），制作了如图统计图（部分信息未给出）．
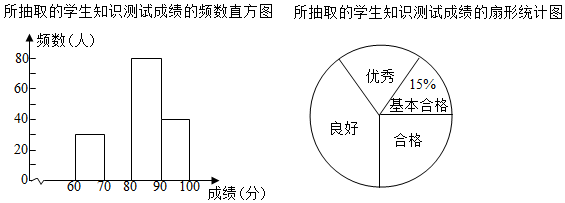
由图中给出的信息解答下列问题：

(1)、求测试成绩为合格的学生人数，并补全频数分布直方图．

(2)、求扇形统计图中“良好”所对应的扇形圆心角的度数．

(3)、这次测试成绩的中位数是什么等级？

(4)、如果全校学生都参加测试，请你根据抽样测试的结果，估计该校获得优秀的学生有多少人？

查看试题解析
19. 如图是由边长为1的小正方形组成的网格，每个小正方形的顶点叫做格点，△ABC的顶点在格点上．

(1)、写出△ABC的面积；

(2)、在网格中找一格点F ，使△DEF与△ABC全等，直接写出满足条件的所有F点坐标；

(3)、利用全等的知识，仅用不带刻度的直尺，在网格中作出△ABC的高CH，保留作图痕迹．

查看试题解析
20. 图1为科研小组研制的智能机器，水平操作台为l，底座AB固定，高AB为50cm，始终与平台l垂直，连杆BC长度为60cm，机械臂CD长度为40cm，点B，C是转动点，AB，BC与CD始终在同一平面内，张角∠ABC可在60°与120°之间（可以达到60°与120°）变化，CD可以绕点C任意转动．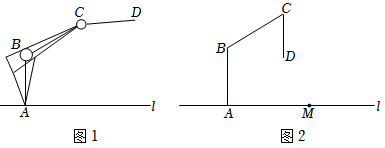

(1)、转动连杆BC，机械臂CD，使张角∠ABC最大，且CD∥AB，如图2，求机械臂臂端D到操作台l的距离DE的长．

(2)、转动连杆BC，机械臂CD，要使机械臂端D能碰到操作台l上的物体M，则物体M离底座A的最远距离和最近距离分别是多少？

查看试题解析
21. 甲，乙两车从甲地驶向B地，并各自匀速行驶，甲车比乙车早行驶2h，并且甲在途中休息了0.5h，如图是甲，乙两车行驶的距离y（km）与时间x（h）的函数图象．

(1)、求出m＝， a＝．

(2)、求甲车休息之后的函数关系式．

(3)、当乙车到达B地时，甲车距B地还有多远？

查看试题解析
22. 已知函数y＝x²+bx+3b（b为常数）．

(1)、若图象经过点（﹣2，4），判断图象经过点（2，4）吗？请说明理由；

(2)、设该函数图象的顶点坐标为（m ， n），当b的值变化时，求m与n的关系式；

(3)、若该函数图象不经过第三象限，当-6≤x≤1时，函数的最大值与最小值之差为16，求b的值．

查看试题解析

23. 根据以下素材，探索完成任务．

如何确定木板分配方案？
素材1	我校开展爱心义卖活动，小艺和同学们打算推销自己的手工制品．他们以每块15元的价格买了100张长方形木板，每块木板长和宽分别为80cm，40cm.
素材2	现将部分木板按图1虚线裁剪，剪去四个边长相同的小正方形（阴影）．把剩余五个矩形拼制成无盖长方体收纳盒，使其底面长与宽之比为3：1．其余木板按图2虚线裁剪出两块木板（阴影是余料），给部分盒子配上盖子．
素材3	义卖时的售价如标签所示：
问题解决
任务1	计算盒子高度	求出长方体收纳盒的高度．
任务2	确定分配方案1	若制成的有盖收纳盒个数大于无盖收纳盒，但不到无盖收纳盒个数的2倍，木板该如何分配？请给出分配方案．
任务3	确定分配方案2	为了提高利润，小艺打算把图2裁剪下来的余料（阴影部分）利用起来，一张矩形余料可以制成一把小木剑，并以5元/个的价格销售．请确定木板分配方案，使销售后获得最大利润．

查看试题解析

尺寸（cm）	160	165	170	175	180
学生人数（人）	1	3	2	2	2