广东省2024年九年级中考模拟数学试卷

试卷更新日期：2024-04-12 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 156000000用科学记数法表示为（）

A、156×10⁶ B、1.56×10⁷ C、1.56×10⁸ D、1.6×10⁸

查看试题解析
2. 将点A（-4，6）向右平移2个单位，向上平移3个单位得到点B，则点B的坐标是（）

A、（-2，4） B、（-2，9） C、（-1，4） D、（-2，3）

查看试题解析
3. 下列运算正确的是（）

A、(-a³)²=a⁶ B、（a²）³＝a⁵ C、2a²•a＝a D、2 $\sqrt{3}$ ﹣ $\sqrt{3}$ ＝ $3 \sqrt{3}$

查看试题解析
4. 某种商品原来每件售价为230元，经过连续两次降价后，该种商品每件售价为196元，设平均每次降价的百分率为x ，根据题意，所列方程正确的是（）

A、230（1﹣x²）＝196 B、230（1﹣x）＝196 C、230（1﹣2x）＝196 D、230（1﹣x）²＝196

查看试题解析
5. 分别标有数字π， $\frac{1}{3}$ ， -2，0，-4的五张卡片中，除数字不同外其他均相同，从中任抽一张，那么抽到非负数的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{1}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 下列图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 不透明的袋子中装有红、绿、黄小球各一个，除颜色外三个小球无其他差别．从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么摸到一个红球一个黄球的概率是（）

A、 $\frac{2}{9}$ B、 $\frac{1}{3}$ C、 $\frac{7}{9}$ D、 $\frac{5}{9}$

查看试题解析
8. 若菱形中两个相邻内角的度数比是2：3，那其中较大的角的度数是（）

A、72° B、108° C、120° D、135°

查看试题解析
9. 一个多边形的内角和为1080°，则这个多边形是（）

A、七边形 B、八边形 C、九边形 D、十边形

查看试题解析
10. 如图，在矩形纸片ABCD中，点E在BC边上，将△CDE沿DE翻折得到△FDE ，点F落在AE上．若CE＝3cm ， AF＝2EF ，则AB＝（）cm ．

A、3 $\sqrt{5}$ B、3 C、 $\sqrt{3}$ D、 $2 \sqrt{5}$

查看试题解析

二、填空题(本大题共5小题，每小题3分,共15分)

11. 分解因式：2ab²﹣2a＝．

查看试题解析
12. 已知反比例函数y＝﹣ $\frac{6}{x}$ 的图象经过点（12，a），则a的值为．

查看试题解析
13. 实数-9的相反数数等于 .

查看试题解析
14. 如图，在△ABC中，AB=8，∠C=90°，∠A=30°，DE是中位线，则DE的长为 .

查看试题解析
15. 如图是二次函数y=ax²+bx+c的图像，对称轴是直线x=2，则下列说法：
①a-b+c-0；②4a+b=0；③ $\frac{a b}{c}$ ﹥0；④16a+5b+2c﹥0，其中正确的是 .

查看试题解析

三、解答题（一）（本大题共3小题，每小题7分，共21分）

16. 解不等式组 ${\begin{array}{l} 5 x - 1 > 3 (x + 1) ① \\ 3 x - 2 ⩽ 2 x + 1 ② \end{array}$ ．

查看试题解析
17. 先化简，再求值： $\frac{x + 1}{x^{2} - 2 x + 1}$ ÷( $\frac{2}{x - 1}$ +1)，其中x= $\sqrt{3}$ +1.

查看试题解析
18. 如图AD是△ABC的角平分线，过点D分别作AC、AB的平行线，交AB于点E，交AC于点F.

(1)、求证：四边形AEDF是菱形.

(2)、若AF＝13，AD＝24.求四边形AEDF的面积.

查看试题解析

四、解答题（二）（本大题共3小题，每小题10分，共30分）

19. 如图，在 $▱ A B C D$ 中， $A C ， B D$ 交于点 $O$ ，点 $E ， F$ 在 $A C$ 上， $A E = C F$ ．

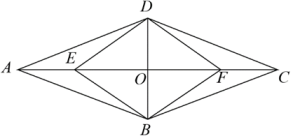(1)、求证：四边形 $E B F D$ 是平行四边形；

(2)、若 $∠ B A C = ∠ D A C ，$ 求证：四边形 $E B F D$ 是菱形．

查看试题解析
20. 为落实“双减”政策，优化作业管理，某中学从全体学生中随机抽取部分学生，调查他们每天完成书面作业的时间t（单位：分钟）．按照完成时间分成五组：A组“t≤45”，B组“45＜t≤60”，C组“60＜t≤75”，D组“75＜t≤90”，E组“t＞90”．将收集的数据整理后，绘制成如下两幅不完整的统计图．
根据以上信息，解答下列问题：

(1)、这次调查的样本容量是 ▲ ，请补全条形统计图；

(2)、在扇形统计图中，A组的圆心角是度，本次调查数据的中位数落在组内；

(3)、若该校有1900名学生，请你估计该校每天完成书面作业不超过90分钟的学生人数．

查看试题解析
21. 某品牌太阳能热水器的实物图和横断面示意图如图所示．已知真空集热管DE与支架CB所在直线相交于点O，且 $O B = O E$ ；支架BC与水平线AD垂直． $A C = 40 cm$ ， $∠ A D E = 30 °$ ， $D E = 190 cm$ ，另一支架AB与水平线夹角 $∠ B A D = 65 °$ ，求OB的长度（结果精确到1cm；温馨提示： $sin 65 ° \approx 0.91$ ， $cos 65 ° \approx 0.42$ ， $tan 65 ° \approx 2.14$ ）

查看试题解析

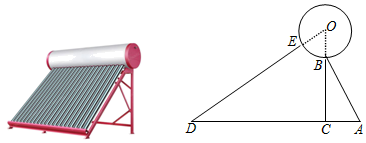
五、解答题（三）（本大题共2小题，每小题12分，共24分）

22. 【问题情境】：
数学活动课上，老师出示了一个问题：如图1，在正方形ABCD中，E是BC的中点，AE⊥EP ， EP与正方形的外角∠DCG的平分线交于P点．试猜想AE与EP的数量关系，并加以证明；

(1)、【思考尝试】：
同学们发现，取AB的中点F ，连接EF可以解决这个问题．请在图1中补全图形，解答老师提出的问题．

(2)、【实践探究】：
希望小组受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形ABCD中，E为BC边上一动点（点E ， B不重合），△AEP是等腰直角三角形，∠AEP＝90°，连接CP ，可以求出∠DCP的大小，请你思考并解答这个问题．

查看试题解析
23. 如图1，在平面直角坐标系中，直线 $y = x + 4$ 与抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 交于A、B两点，点A在x轴上，点B在y轴上．设抛物线与x轴的另一个交点为点C ．

(1)、求该抛物线的解析式；

(2)、若点M是抛物线对称轴上的一个动点，当 $M C + M B$ 的值最小时，求点M的坐标；

(3)、P是抛物线上一动点（不与点A、B重合），如图2，若点P在直线 $A B$ 上方，连接 $O P$ 交 $A B$ 于点D ，
求 $\frac{P D}{O D}$ 的最大值；

查看试题解析