广东省湛江市廉江市2024年中考一模数学试卷

试卷更新日期：2024-04-12 类型：中考模拟

进入出卷网下载

一、选择题：本题共有10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有项符合题目要求．

1. 下列四个数中，负整数是（）

A、2024 B、 $- 3.14$ C、0 D、 $- 3$

查看试题解析
2. 第33届夏季奥运会将于2024年7月26日至8月11日在法国巴黎举行，下列巴黎奥运会项目图标中，轴对称图形是（）

A、 B、 C、 D、

查看试题解析
3. 九（2）班大部分学生的年龄都是15周岁，这里的15周岁指的是九（2）班全体学生年龄的（）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
4. 如图， $C M ∥ B N$ ， $∠ C = 45 °$ ， $∠ B = 20 °$ ，则 $∠ A$ 的度数为（）

A、 $45 °$ B、 $35 °$ C、 $25 °$ D、 $20 °$

查看试题解析
5. 下列运算中，正确的是（）

A、 $a^{5} - a^{3} = a^{2}$ B、 $a^{4} \cdot a^{3} = a^{7}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
6. 有理数 $a, b$ 在数轴上的对应点如图所示，则下列式子一定成立的是（）

A、 $a < - 3$ B、 $| a | < b$ C、 $a + b > 0$ D、 $| a b | > 1$

查看试题解析
7. 一元一次不等式组 ${\begin{array}{l} 2 x - 3 < 1, \\ 5 x + 1 \geq 4 x \end{array}$ 的解集是（）

A、 $x < 2$ B、 $1 \leq x < 2$ C、 $- 1 \leq x < 2$ D、 $x \leq - 1$

查看试题解析
8. 若关于 $x$ 的一元二次方程 $k x^{2} + 4 x - 4 = 0$ 有实数根，则 $k$ 的取值范围是（）

A、 $k \geq - 1$ B、 $k \leq - 1$ C、 $k > - 1$ 且 $k \neq 0$ D、 $k \geq - 1$ 且 $k \neq 0$

查看试题解析
9. 如图，四边形 $A B C D$ 是菱形，过点 $B$ 作 $B E ⊥ A B$ 交对角线 $A C$ 于点 $E$ ．若 $A E = 8, A B = 7$ ，则 $E C$ 的长为（）

A、 $\frac{17}{4}$ B、 $\frac{17}{2}$ C、 $\frac{49}{8}$ D、 $\frac{15}{8}$

查看试题解析
10. 如图，在正方形 $A B C D$ 中， $A B = 4, A N ⊥ D M$ ．则下列结论：① $△ D A G ∽ △ A N B$ ；② $S_{△ A D G} = S_{四边形 B M G N}$ ；③连接 $M N, D N$ ，若 $△ D M N$ 的面积为 $\frac{13}{2}$ ，则 $A N$ 的长为5．其中正确的结论是（）

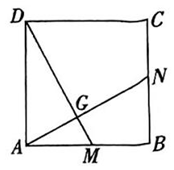A、①② B、①②③ C、①③ D、②③

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分．

11. 因式分解： $x^{2} - 2 x$ = ．

查看试题解析
12. 如图1，这是某公园里采用的六角形空窗，其轮廓是一个正六边形，图2是该六角形空窗的示意图，则它的内角和为．

查看试题解析
13. 若 ${(m - 5)}^{2} + \sqrt{n - 11} = 0$ ，则以 $m, n$ 为边长的等腰三角形的周长为．

查看试题解析
14. 如图，直线 $O A : y = k x$ 与反比例函数 $y = \frac{12}{x}$ 的图象交于点 $A (3, m), B$ ，则点 $B$ 的坐标为．

查看试题解析
15. 如图， $A B$ 是 $⊙ O$ 的直径， $A B = 2$ ， $D$ 是 $⊙ O$ 外的一点， $C$ 是线段 $D A$ 的中点，连接 $B D$ 交 $⊙ O$ 于点 $E$ ，且满足四边形 $O A C E$ 是矩形，则阴影部分的面积为．

查看试题解析

三、解答题（一）：本大题共3小题，第16题10分，第17、18题各7分，共24分．

16.

(1)、计算： ${(π - 2024)}^{0} + 4 c o s 30 ° + | \sqrt{12} - 4 |$ ．

(2)、先化简，再求值： $(1 - \frac{x}{x + 2}) \div \frac{x^{2} - 2 x}{x^{2} - 4}$ ，其中 $x = \sqrt{5}$ ．

查看试题解析
17. 如图，在 $▱ A B C D$ 中， $A D = 12, A B = 6$ ．

(1)、用尺规作图法作 $∠ A D C$ 的平分线 $D N$ ，交 $B C$ 于点 $M$ ，交 $A B$ 的延长线于点 $N$ ．（标明字母，保留作图痕迹，不要求写作法）

(2)、在（1）的条件下，求 $B N$ 的长．

查看试题解析
18. 安铺镇是广东四大古镇之一，它始建于明代1444年，迄今为止已有500多年的历史．九（1）班的小明要测量安铺镇文阁塔的高度，如图，小明在文阁塔前的平地上选择一点 $A$ ，在点 $A$ 和文阁塔之间选择一点 $B$ ，测得 $A B = 38 m$ ，用测角仪在 $A$ 处测得文阁塔顶部 $E$ 的仰角为 $30 °$ ，在 $B$ 处测得仰角为 $60 °$ ，已知测角仪的高 $A C = 1 m$ ．请你帮小明计算出文阁塔 $E F$ 的高度．（结果保留根号）

查看试题解析

四、解答题（二）：本大题共3小题，每小题9分，共27分．

19. 某市流行一种簪花，色彩绚丽美观，展现了人们的朴素美和对生活的热爱．随着簪花文化的传播，也带动了簪花的销售，某商场购进一批成本为每件30元的簪花，销售时单价不低于成本价，且不高于50元．据市场调查、分析，发现该簪花每天的销售量 $y$ （件）与销售单价 $x$ （元）之间满足一次函数关系，且当单价为35元时，可销售90件；当单价为45元时，可销售70件．

(1)、求出 $y$ 与 $x$ 之间的函数关系式．

(2)、当销售单价定为多少时，才能使销售该种簪花每天获得的利润 $W$ （元）最大？最大利润是多少？

查看试题解析
20. 综合与实践
主题：研究旋转的奥妙．
素材：一张等边三角形硬纸板和一根木棍．
步骤：如图，将一根木棍 $A M$ 放在等边三角形硬纸板 $A P Q$ 上，木棍一端 $A$ 与等边三角形的顶点重合，点 $M$ 在 $P Q$ 上（不与点 $P, Q$ 重合），将木棍 $A M$ 绕点 $M$ 顺时针方向旋转 $60 °$ ，得到线段 $M N$ ，点 $A$ 的对应点为 $N$ ，连接 $Q N$ ．
猜想与证明：

(1)、直接写出线段 $P M$ 与线段 $Q N$ 的数量关系．

(2)、证明（1）中你发现的结论．

查看试题解析
21. 环保是当今社会人们最关注的话题之一，某校为了解碳中和、食品安全等知识的普及情况，随机抽取了部分学生进行问卷调查，问卷有四个选项（每位被调查的学生必须且只能选一项）：A．不了解；B．了解较少；C．了解；D．非常了解．并将调查结果绘制成了以下两幅不完整的统计图．
请根据统计图，回答下列问题．

(1)、本次共抽取了 ▲名学生，并根据调查信息补全条形统计图．

(2)、若该校共有1600名学生，估计“非常了解”的学生共有名．

(3)、在被调查的“非常了解”的学生中，有四名学生（2名男生和2名女生）来自九（1）班，班主任想从这四名学生中任选两名去参加环保知识竞赛．请你用列表法或画树状图法，求出被选中的两人恰好是一男一女的概率．

查看试题解析

五、解答题（三）：本大题共2小题，每小题12分，共24分．

22. 综合探究
如图1， $△ A B C$ 是 $⊙ O$ 的内接三角形， $P$ 是 $⊙ O$ 上的一点，连接 $A P$ 交 $B C$ 于点 $M$ ，点 $N$ 在 $A M$ 上，满足 $∠ A N B - ∠ B N P = ∠ A C B$ ， $N Q ∥ A C$ 交 $B C$ 于点 $Q$ ， $B M = N Q$ ，连接 $B P, P Q$ ．

(1)、求证： $P B = P N$ ．

(2)、求证： $△ B P M ≌ △ N P Q$ ．

(3)、如图2， $A P$ 为 $⊙ O$ 的直径，设 $∠ A C B = α$ ，当 $\overset{⌢}{A B}$ 的长为2时，求 $\overset{⌢}{A C}$ 的长．

查看试题解析
23. 综合运用
已知抛物线 $C_{1} : y = a x^{2} + 2 a x + a - \frac{2}{3}$ ．

(1)、抛物线 $C_{1}$ 的对称轴为直线．

(2)、如图，将抛物线 $C_{1}$ 平移使其顶点是坐标原点 $O$ ，得到抛物线 $C_{2}$ ，且抛物线 $C_{2}$ 过点 $A (- 2, - 2), B$ （点 $B$ 在点 $A$ 的左侧）．若 $△ A B O$ 的面积为4，求点 $B$ 的坐标．

(3)、在（2）的条件下，直线 $l_{1} : y = k x - 2$ 与抛物线 $C_{2}$ 交于点 $M, N$ ，分别过点 $M, N$ 的两条直线 $l_{2}, l_{3}$ 交于点 $P$ ，且 $l_{2}, l_{3}$ 与 $y$ 轴不平行，当直线 $l_{2}, l_{3}$ 与抛物线 $C_{2}$ 均只有一个公共点时，请说明点 $P$ 在一条定直线上．

查看试题解析