广东省阳江市阳西县2024年中考一模数学试卷

试卷更新日期：2024-04-12 类型：中考模拟

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 下列运算中正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{2} \cdot a^{4} = a^{8}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
3. 要使代数式 $\frac{\sqrt{x - 2}}{3}$ 有意义，则x的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 2$ C、 $x > 2$ D、 $x \leq 2$

查看试题解析
4. 2023年10月26日神舟十七号载人飞船发射取得圆满成功，我国载人航天工程发射任务实现30战30捷，航天员在中国空间站俯瞰地球的高度约为400000米，将400000用科学记数法表示应为（）

A、 $4 \times 1 0^{5}$ B、 $4 \times 1 0^{6}$ C、 $40 \times 1 0^{4}$ D、 $0.4 \times 1 0^{6}$

查看试题解析
5. 若某三角形的三边长分别为3，4，m，则m的值可以是（）

A、1 B、5 C、7 D、9

查看试题解析
6. 多项式 $2 a^{2} b - a b^{2} - a b$ 的项数及次数分别是（）

A、3；3 B、3；2 C、2；3 D、2；2

查看试题解析
7. 一副直角三角板按如图所示的方式摆放，其中点C在FD的延长线上，且AB∥FC ，则∠CBD的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
8. 在平面直角坐标系中，点 $P (- 3, 2)$ 关于 $x$ 轴的对称点在：（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 若 $n - m = 2$ ，则 $\frac{m^{2} - n^{2}}{m} \cdot \frac{2 m}{m + n}$ 的值是（）

A、4 B、2 C、 $- 2$ D、 $- 4$

查看试题解析
10. 如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF＝3，则菱形ABCD的周长为（）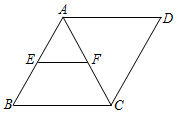

A、24 B、18 C、12 D、9

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分．

11. 因式分解：x²﹣3x= ．

查看试题解析
12. 若一个多边形的内角和为 $540 °$ ，则这个多边形的边数是．

查看试题解析
13. 若 ${(x + 4)}^{2} + \sqrt{y - 3} = 0$ ，则 $x + y =$ ．

查看试题解析
14. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 13$ ， $t a n ∠ A = \frac{5}{12}$ ，则 $B C$ 的长为．

查看试题解析
15. 若一元二次方程 $k x^{2} - 3 x + 1 = 0$ 有两个相等的实数根，则 $k$ 的值是．

查看试题解析
16. 一个盒子里放有草莓味、苹果味的两种糖各1块，另一个盒子里放有草莓味、苹果味、葡萄味的三种糖各1块，糖的外形相同．小亮从两个盒子中各随机取出一块糖，则两块糖是不同味的概率是．

查看试题解析

三、解答题（一）：本大题共3小题，第17题10分，第18、19题各7分，共24分．

17.

(1)、计算： ${(\frac{1}{2})}^{- 2} + | - 3 | - \sqrt{25}$ ；

(2)、解不等式： $2 x - 1 > \frac{3 x - 1}{2}$ ．

查看试题解析
18. 腊味食品深受广大群众的喜爱．春节期间，某单位打算为员工购买腊肉和香肠作为新年福利．该单位花费39000元购买了200袋腊肉，100袋香肠，已知5袋腊肉和4袋香肠的售价相同，求每袋腊肉和香肠的售价分别是多少元？

查看试题解析
19. 某校为了解该校学生一周的课外劳动情况，随机抽取部分学生调查了他们一周的课外劳动时间，将数据进行整理并制成如下统计图．
请根据图中提供的信息，解答下面的问题：

(1)、图1中 $m =$ ，本次调查数据的中位数是 $h$ ，本次调查数据的众数是 $h$ ；

(2)、该校共有 $2000$ 名学生，请根据统计据，估计该校学生一周的外劳动时间不小于 $3 h$ 的人数．

查看试题解析

四、解答题（二）：本大题共3小题，每小题8分，共24分．

20. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ．

(1)、实践与操作：用尺规作图法作 $∠ B A C$ 的平分线交 $B C$ 于点D（保留作图痕迹，不要求写作法）；

(2)、应用与计算：在（1）的条件下，过点D作 $D E ⊥ A B$ 于点E ，若 $A B = 10$ ， $△ A D B$ 的面积为15，求 $C D$ 的长．

查看试题解析
21. 综合与实践
主题：制作圆锥形生日帽．
素材：一张圆形纸板、装饰彩带．
步骤1：如图1，将一个底面半径为r的圆锥侧面展开，可得到一个半径为l、圆心角为 $n °$ 的扇形．制作圆锥形生日帽时，要先确定扇形的圆心角度数，再度量裁剪材料．
步骤2：如图2，把剪好的纸板粘合成圆锥形生日帽．
在制作好的生日帽中， $A B = 6 c m$ ， $l = 6 c m$ ， C是 $P B$ 的中点，现要从点A到点C再到点A之间拉一条装饰彩带，求彩带长度的最小值．

查看试题解析
22. 如图所示，一次函数 $y_{1} = - x + m$ 与反比例函数 $y_{2} = \frac{k}{x}$ 相交于点A和点 $B (3 ， - 1)$ ．

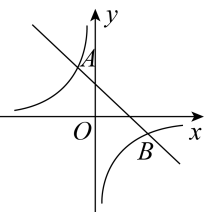(1)、求m的值和反比例函数解析式；

(2)、当 $y_{1} > y_{2}$ 时，求x的取值范围．

查看试题解析

五、解答题（三）：本大题共2小题，每小题12分，共24分．

23. 综合探究：如图， $⊙ O$ 是四边形 $A B C D$ 的外接圆，直径为10，过点D作 $D P ⊥ A B$ ，交 $B A$ 的延长线于点P ， $A D$ 平分 $∠ P A C$ ．

(1)、在图1中，若 $A C$ 为 $⊙ O$ 的直径，求证： $P D$ 与 $⊙ O$ 相切；

(2)、在图1中，若 $A C$ 为 $⊙ O$ 的直径， $\overset{⌢}{A B} = \overset{⌢}{B C}$ ，求 $∠ P D C$ 的度数；

(3)、在图2中，若 $B C = C D$ ，求证： $A B + A D = A C$ ．

查看试题解析
24. 已知二次函数图象的顶点坐标为 $A (1 ， 4)$ ，且与x轴交于点 $B (- 1 ， 0)$ ．

(1)、求二次函数的表达式；

(2)、如图，将二次函数图象绕x轴的正半轴上一点 $P (m ， 0)$ 旋转 $180 °$ ，此时点A、B的对应点分别为点C、D．
①连结 $A B 、 B C 、 C D 、 D A$ ，当四边形 $A B C D$ 为矩形时，求m的值；
②在①的条件下，若点M是直线 $x = m$ 上一点，原二次函数图象上是否存在一点Q，使得以点B、C、M、Q为顶点的四边形为平行四边形，若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析