浙江省嘉兴市桐乡市2023-2024学年八年级下学期3月月考数学试题
试卷更新日期:2024-04-12 类型:月考试卷
一、选择题:(每题3分共30分)
-
1. 二次根式中字母x的取值范围是( )A、 B、 C、 D、2. 若是关于的一元二次方程的一个根,则的值为( )A、 B、 C、10 D、93. 小红在计算时遇到以下情况,结果正确的是( )A、 B、 C、 D、4. 用配方法解一元二次方程 , 配方后可变形为( )A、 B、 C、 D、5. 已知a是方程的一个解,则的值为( )A、2023 B、2022 C、2021 D、20206. 2017年5月,20国青年评选出了中国的“新四大发明”:高铁、支付宝、共享单车和网购.某共享单车公司计划2018年连续3个月对合肥投放新型共享单车,计划第一个月投放3000台,第3个月投放6000台,每月按相同的增长率投放,设增长率为x , 则可列方程( )A、3000(1+x)2=6000 B、3000(1+x)+3000(1+x)2=6000 C、3000(1-x)2=6000 D、3000+3000(1+x)+3000(1+x)2=60007. 已知两个关于x的一元二次方程 , 其中 . 下列结论错误的是( )A、若方程M有两个相等的实数根,则方程N也有两个相等的实数根 B、若方程M有一个正根和一个负根,则方程N也有一个正根和一个负根 C、若5是方程M的一个根,则是方程N的一个根 D、若方程M和方程N有一个相同的根,则这个根一定是8. 已知图2是由图1七巧板拼成的数字“0”,已知正方形ABCD的边长为4,则六边形EFGHMN的周长为( )
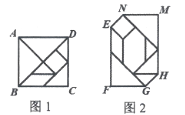 A、 B、 C、 D、129. 三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法,以方程即为例说明,记载的方法是:构造如下图,大正方形的面积是 . 同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此 . 则在下面四个构图中(网格中每个小正方形边长为1个单位),能正确说明方程:解法的构图是( )
A、 B、 C、 D、129. 三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法,以方程即为例说明,记载的方法是:构造如下图,大正方形的面积是 . 同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此 . 则在下面四个构图中(网格中每个小正方形边长为1个单位),能正确说明方程:解法的构图是( )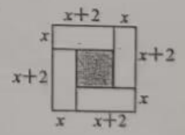 A、
A、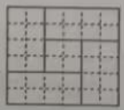 B、
B、 C、
C、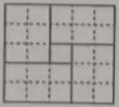 D、
D、 10. 若 , 是方程的两实数根,则的值为( )A、5 B、6 C、7 D、8
10. 若 , 是方程的两实数根,则的值为( )A、5 B、6 C、7 D、8二、填空题:(每小题3分共30分)
-
11. 化简: .12. 若实数的小数部分为a , 则 .13. 已知,x,y为实数,且满足 , 那么=.14. 实数a , b在数轴上的位置如图所示,化简: .
 15. 若一元二次方程有一根为 , 则的值为 .16. m=时,关于x的方程是一元二次方程.17. 有一人利用手机发短信,获得他信息的人也按他的发送人数发送该条短信,经历两轮短信的发送,共有110人的手机获得该条短信.设每人给y人发短信,则可列方程 .18. 关于x的方程有实数根,则a的取值范围 .19. 阅读材料:如果两个正数a、b , 即 , , 则有下面的不等式 , 当且仅当时取到等号.我们把叫做正数a、b算术平均数,把叫做正数a、b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.根据上述材料,若 , 则y最小值为 .20. 如图,在平面直角坐标系中,点 , 点 , 若动点从坐标原点出发,沿轴正方向匀速运动,运动速度为个单位长度每秒,设点运动时间为秒,当是等腰三角形时,的值为 .
15. 若一元二次方程有一根为 , 则的值为 .16. m=时,关于x的方程是一元二次方程.17. 有一人利用手机发短信,获得他信息的人也按他的发送人数发送该条短信,经历两轮短信的发送,共有110人的手机获得该条短信.设每人给y人发短信,则可列方程 .18. 关于x的方程有实数根,则a的取值范围 .19. 阅读材料:如果两个正数a、b , 即 , , 则有下面的不等式 , 当且仅当时取到等号.我们把叫做正数a、b算术平均数,把叫做正数a、b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.根据上述材料,若 , 则y最小值为 .20. 如图,在平面直角坐标系中,点 , 点 , 若动点从坐标原点出发,沿轴正方向匀速运动,运动速度为个单位长度每秒,设点运动时间为秒,当是等腰三角形时,的值为 .
三、解答题:共40分
-
21.(1)、计算:(2)、解方程22. 如图,在等腰三角形ABC中,AB=AC= ,BC=.
 (1)、求△ABC的面积;(2)、过点 B作AC边的高线 BH,求 BH的长.23. 关于x的方程有两个实数根 , . 若 , 求m的值;24. 每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元,在标价8000元的基础上打9折销售.(1)、现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?(2)、据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售相同的沙发,其成本、标价与甲卖家一致,以前每周可售出8套,现乙卖家先将标价提高 ,再大幅降价 元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了 ,这样一天的利润达到了50000元,求 的值.25. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)、求△ABC的面积;(2)、过点 B作AC边的高线 BH,求 BH的长.23. 关于x的方程有两个实数根 , . 若 , 求m的值;24. 每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元,在标价8000元的基础上打9折销售.(1)、现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?(2)、据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售相同的沙发,其成本、标价与甲卖家一致,以前每周可售出8套,现乙卖家先将标价提高 ,再大幅降价 元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了 ,这样一天的利润达到了50000元,求 的值.25. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)、如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)、如果△ABC是等边三角形,试求这个一元二次方程的根.
26. 如图,在矩形中, , , 点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动,当其中一点到达终点运动即停止.设运动时间为秒. (1)、在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;(2)、在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;(3)、取的中点 , 运动过程中,当时,求的值;
(1)、在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;(2)、在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;(3)、取的中点 , 运动过程中,当时,求的值;