浙江省杭州市萧山区萧山城区九年级8校联考2023-2024学年九年级下学期3月月考数学试题

试卷更新日期：2024-04-12 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 在下列选项实数中，是无理数的是（）

A、 $- 2$ B、 $2 π$ C、 $\sqrt{4}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{10} \div a^{2} = a^{5}$ B、 ${(a^{2})}^{3} = a^{6}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 $a^{2} + a^{2} = a^{4}$

查看试题解析
3. 2024年某市计划重点工程建设项目投资总额为5045亿元，其中5045亿用科学记数法表示为（）

A、 $50.45 \times 1 0^{10}$ B、 $0.5045 \times 1 0^{12}$ C、 $5.045 \times 1 0^{11}$ D、 $5.045 \times 1 0^{10}$

查看试题解析
4. 下列图标中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 在学校举办的学习强国演讲比赛中，李华根据九位评委所给的分数制作了如下表格：
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（　　）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
6. 若 $b < 0$ ，则二次函数 $y = x^{2} + b x - 1$ 的图象的顶点在（）

A、第一象限； B、第二象限； C、第三象限； D、第四象限

查看试题解析
7. 下面的三个问题中都有两个变量：
①汽车从A地匀速行驶到B地，汽车的剩余路程y与行驶时间x；②将水箱中的水匀速放出，直至放完，水箱中的剩余水量y与放水时间x；③用长度一定的绳子围成一个矩形，矩形的面积y与一边长x，其中，变量y与变量x之间的函数关系可以利用如图所示的图象表示的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
8. 如图，点A在反比例函数y＝ $\frac{4}{x}$ （x＞0）的图象上，点B在反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象上，AB∥x轴，点C在x轴上，△ABC的面积为3，则k的值为（）

A、1 B、﹣1 C、2 D、﹣2

查看试题解析
9. 如图，四边形 $A B C D$ 为矩形，点 $E$ 在边 $C D$ 上， $D E = 2 C E$ ， $⊙ O$ 与四边形 $A B E D$ 的各边都相切， $⊙ O$ 的半径为 $x$ ， $△ B C E$ 的内切圆半径为 $y$ ，则 $x : y$ 的值为（）

A、 $2$ B、 $\frac{8}{3}$ C、 $3$ D、 $\frac{10}{3}$

查看试题解析
10. 对于给定的两个函数，任取自变量x的一个值，当 $x < 0$ 时，它们对应的函数值互为相反数；当 $x \geq 0$ 时，它们对应的函数值相等，我们称这样的两个函数互为“阴阳函数”．例如：一次函数 $y = x + 2$ ，它的“阴阳函数”为 $y = {\begin{array}{l} - x - 2 (x < 0) \\ x + 2 (x \geq 0) \end{array}$ ．若点 $P (m, 2)$ 在二次函数 $y = x^{2} + 2 x - 3$ 的“阴阳函数”的图象上时，则m的值为（）

A、 $- 1 + \sqrt{6}$ 或 $- 1 - \sqrt{2}$ B、 $- 1 + \sqrt{2}$ C、 $- 1 - \sqrt{6}$ 或 $- 1 + \sqrt{2}$ D、 $- 1 - \sqrt{6}$

查看试题解析

二、填空题（每小题4分，共24分，第16题每空2分）

11. 计算 $\sqrt{18} - \sqrt{8}$ 的结果是．

查看试题解析
12. 分解因式： $9 a - a b^{2} =$

查看试题解析
13. 若a、b互为相反数，m、n互为倒数，则 $2024 a + 2023 b + m n b$ 的值为．

查看试题解析
14. 已知圆锥的轴截面是边长为6的等边三角形，则这个圆锥的侧面积是.

查看试题解析
15. 已知抛物线 $y = a x^{2} + b x + c$ 与直线 $y = m x + n$ 的交点横坐标分别为1，4，则抛物线 $y = a x^{2} + (b - m) x$ 的对称轴为直线 $x =$ ．

查看试题解析
16. 如图，在 $R t △ A B C$ 中，D为斜边 $A C$ 的中点，点E在边 $A B$ 上，将 $△ B C E$ 沿 $C E$ 叠至 $△ F C E$ ．若 $E F$ 的延长线经过点D ， $C F$ 平分 $∠ A C B$ ， $B E = 1$ ，则 $\frac{D E}{A E}$ 的值为， $A B$ 的长为．

查看试题解析

三、解答题（第17-19题每小题6分，第20、21题每小题8分，第22、23题每小题10分，第24题12分，共66分）

17. 设一元二次方程 $x^{2} + b x + c = 0$ ，在下面的三组条件中选择其中一组b ， c的值，使这个方程有两个不相等的实数根，并解这个方程．
① $b = 2$ ， $c = 1$ ；② $b = 5$ ， $c = 6$ ；③ $b = 4$ ， $c = 5$ ．

查看试题解析
18. 为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图所示的统计图，已知“查资料”的人数是 $40$ 人．
请你根据以上信息解答下列问题：

(1)、本次随机抽取的学生共有人；

(2)、在扇形统计图中，“玩游戏”对应的百分比为，圆心角度数是度；

(3)、补全条形统计图；

(4)、该校共有学生 $2100$ 人，估计每周使用手机时间在 $2$ 小时以上（不含 $2$ 小时）的人数．

查看试题解析
19. 如图，在 $▱ A B C D$ 中，点 $O$ 是对角线 $A C$ 的中点．某数学学习小组要在 $A C$ 上找两点 $E$ ， $F$ ，使四边形 $B E D F$ 为平行四边形，现总结出甲、乙两种方案如下：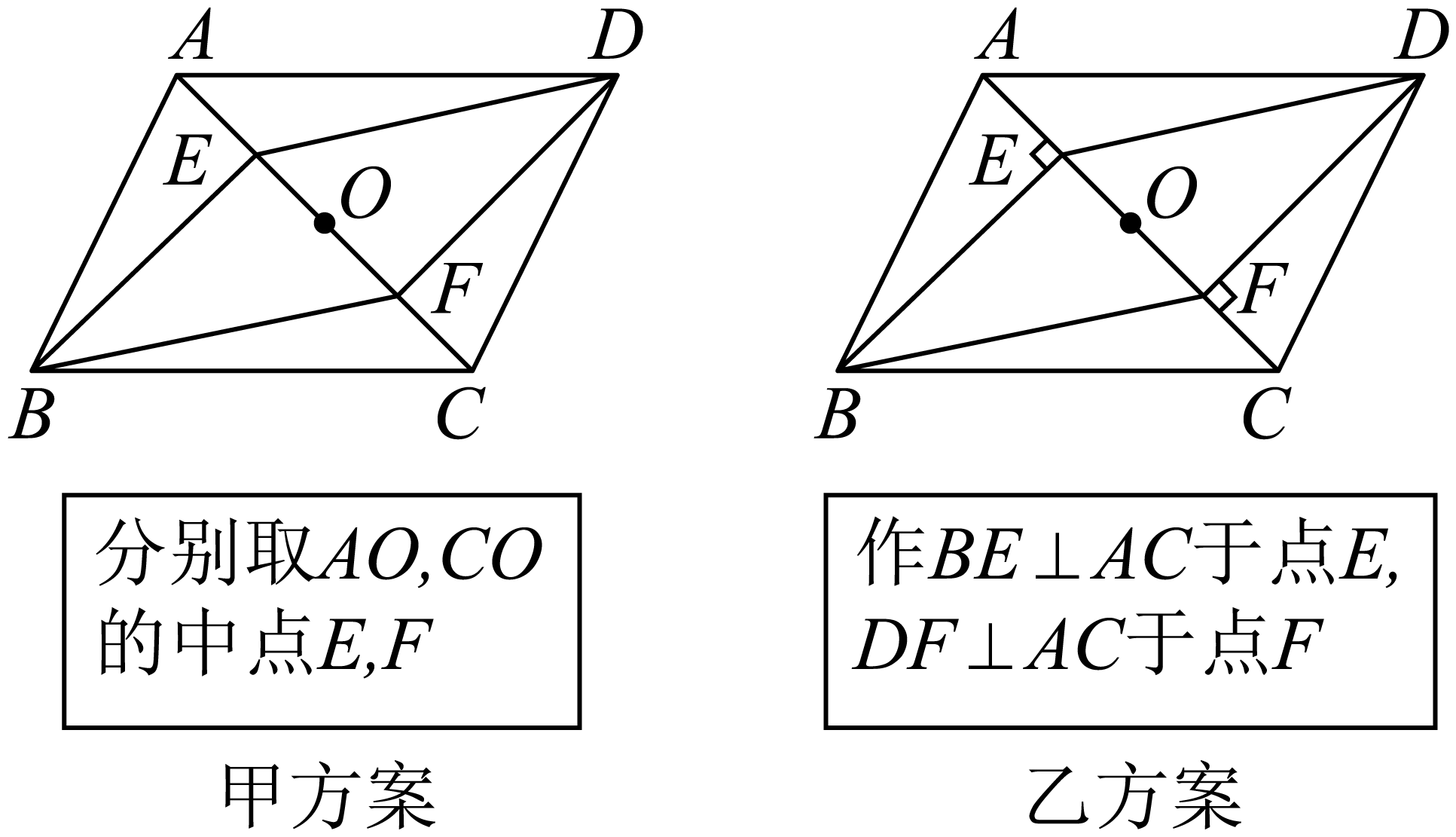
请回答下列问题：

(1)、以上方案能得到四边形 $B E D F$ 为平行四边形的是▲ ，选择其中一种并证明，若不能，请说明理由；

(2)、若 $E F = 2 A E$ ， ${S_{△}}_{A E D} = 6$ ，求 $▱ A B C D$ 的面积

查看试题解析
20. 在直角坐标系中，已知 $k_{1} k_{2} \neq 0$ ，设函数 $y_{1} = \frac{k_{1}}{x}$ 与函数 $y_{2} = k_{2} (x - 2) + 5$ 的图象交于点 $A$ 和点 $B$ ．已知点 $A$ 的横坐标是2，点 $B$ 的纵坐标是 $- 4$ ．

(1)、求 $k_{1} ， k_{2}$ 的值．

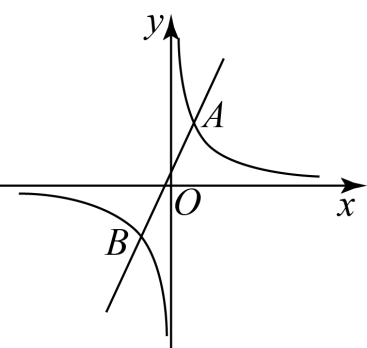(2)、过点 $A$ 作 $y$ 轴的垂线，过点 $B$ 作 $x$ 轴的垂线，在第二象限交于点 $C$ ；过点 $A$ 作 $x$ 轴的垂线，过点 $B$ 作 $y$ 轴的垂线，在第四象限交于点 $D$ ．求证：直线 $C D$ 经过原点．

查看试题解析
21. 假定甲、乙、丙三地依次在一条直线上，甲乙两地间的距离为280km，乙丙两地之间的距离为140km．一艘游轮从甲地出发前往丙地，途中经过乙地停留时，一艘货轮也沿着同样的线路从甲地出发前往丙地．已知游轮的速度为 $20 k m / h$ ，游轮从甲地到达丙地共用了23小时．
若将游轮行驶的时间记为t（h），两艘轮船距离甲地的路程s（km）关于t（h）的图象如图所示（游轮在停靠前后的行驶速度不变）

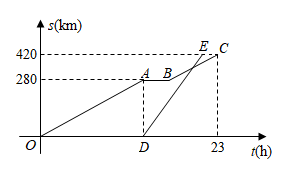(1)、写出游轮从甲地到乙地所用的时长；游轮在乙地停留的时长；

(2)、直接写出游轮在行驶的过程中s关于t的函数解析式；

(3)、若货轮比游轮早36分钟到达丙地，则货轮出发后几小时追上游轮？

查看试题解析
22. 如图，在正方形 $A B C D$ 中， $E$ 是边 $B C$ 上一动点（不与点 $B, C$ 重合），连接 $D E$ ，点 $C$ 关于直线 $D E$ 的对称点为 $C^{'}$ ，连接 $A C^{'}$ 并延长交直线 $D E$ 于点 $P$ ，过点 $D$ 作 $D F ⊥ A P$ 于 $F$ ．

(1)、①依题意补全图形；
②求 $∠ F D P$ 的度数；

(2)、连接 $B P$ ，请用等式表示线段 $B P$ 与线段 $A F$ 之间的数量关系，并证明．

查看试题解析
23. 已知抛物线 $y = x^{2} - 2 m x + m^{2} - 2$ 与直线 $x = - 2$ 交于点 $P .$

(1)、若抛物线经过 $(- 1, - 2)$ 时，求抛物线解析式；

(2)、设P点的纵坐标为 $y_{p}$ ，当 $y_{p}$ 取最小值时，抛物线上有两点 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ ， $x_{1} < x_{2} < - 2$ ，比较 $y_{1}$ 与 $y_{2}$ 的大小；

(3)、若线段 $A B$ 两端点坐标分别是 $A (0, 2)$ ， $B (2, 2)$ ，当抛物线与线段 $A B$ 有公共点时，求出m的取值范围．

查看试题解析
24. 如图， $A B$ 为 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E ，点F在 $A B$ 上，连结 $D F$ 并延长交 $⊙ O$ 与点G ，连结 $B G ， C G$ ， $C G = F G$ ．

(1)、如图1，求证： $△ B C G ≌ △ B F G$ ；

(2)、如图2， $B G$ 与 $C D$ 交于点N ，过点F作 $B G$ 的平行线交 $C D$ 于点M ，若 $N E = a$ ，求 $D M$ ．（用含a的代数式表示）

(3)、如图3，在（2）的条件下，连结 $G E$ ，若 $△ E F G$ 与 $△ D F M$ 的面积相等，求 $c o s ∠ A B C$ 的值．

查看试题解析

平均数	中位数	众数	方差
8.5	8.3	8.1	0.15