浙江省湖州市长兴县龙山共同体2023-2024学年七年级下学期3月月考数学试题
试卷更新日期:2024-04-12 类型:月考试卷
一、选择题(本题共10小题,每小题3分,共30分)
-
1. 下列方程是二元一次方程的是( )A、 B、 C、 D、2. 下列图形中,由能得到的是( )A、
 B、
B、 C、
C、 D、
D、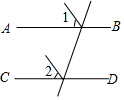 3. 下列说法正确的是( )A、两点之间,直线最短 B、不相交的两条直线叫做平行线 C、平面内,过一点有且只有一条直线与已知直线垂直 D、直线外一点到这条直线的垂线段叫做点到直线的距离4. 小亮用28元钱买了甲、乙两种水果,甲种水果每千克4元,乙种水果每千克6元,且乙种水果比甲种水果少买了2千克,求小亮两种水果各买了多少千克?设小亮买了甲种水果x千克,乙种水果y千克,则可列方程组为( )A、 B、 C、 D、5. 将方程 变形为用含 的代数式表示 为 ( )A、 B、 C、 D、6. 如图,直线的顶点B , C分别在上,若 , 则的大小为( )
3. 下列说法正确的是( )A、两点之间,直线最短 B、不相交的两条直线叫做平行线 C、平面内,过一点有且只有一条直线与已知直线垂直 D、直线外一点到这条直线的垂线段叫做点到直线的距离4. 小亮用28元钱买了甲、乙两种水果,甲种水果每千克4元,乙种水果每千克6元,且乙种水果比甲种水果少买了2千克,求小亮两种水果各买了多少千克?设小亮买了甲种水果x千克,乙种水果y千克,则可列方程组为( )A、 B、 C、 D、5. 将方程 变形为用含 的代数式表示 为 ( )A、 B、 C、 D、6. 如图,直线的顶点B , C分别在上,若 , 则的大小为( ) A、 B、 C、 D、7. 如图,为一条长方形纸带, , 将沿折叠,A , D两点分别与 , 对应,若 , 则的度数是( )
A、 B、 C、 D、7. 如图,为一条长方形纸带, , 将沿折叠,A , D两点分别与 , 对应,若 , 则的度数是( ) A、 B、 C、 D、8. 在一定范围内弹簧的长度与它所挂物体的重量之间满足关系式 . 已知挂重为时,弹簧长;挂重为时,弹簧长;那么当弹簧长时,挂重为( )A、 B、 C、 D、9. 如图,正方形由四个相同的大长方形、四个相同的小长方形以及一个小正方形组成,其中四个大长方形的长和宽分别是小长方形长和宽的3倍,若中间小正方形的面积为1,则大正方形的面积是( )
A、 B、 C、 D、8. 在一定范围内弹簧的长度与它所挂物体的重量之间满足关系式 . 已知挂重为时,弹簧长;挂重为时,弹簧长;那么当弹簧长时,挂重为( )A、 B、 C、 D、9. 如图,正方形由四个相同的大长方形、四个相同的小长方形以及一个小正方形组成,其中四个大长方形的长和宽分别是小长方形长和宽的3倍,若中间小正方形的面积为1,则大正方形的面积是( )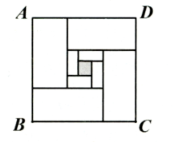 A、25 B、36 C、49 D、8110. 如图, , 点E为上方一点,分别为的角平分线,若 , 则的度数为( )
A、25 B、36 C、49 D、8110. 如图, , 点E为上方一点,分别为的角平分线,若 , 则的度数为( )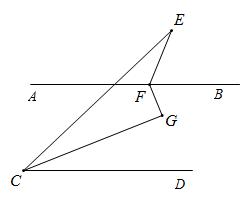 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共6小题,每小题4分,共24分)
-
11. 解二元一次方程组时,小华用加减消元法消去未知数y , 按照他的思路,用①+②得到的方程是 .12. 如图, , , 若∠B=72°,则∠D的度数是.
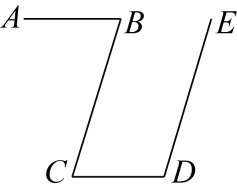 13. 如图,在一块长为 , 宽为的长方形草地上,有一条路宽为的小路,这块草地的绿地面积为 .
13. 如图,在一块长为 , 宽为的长方形草地上,有一条路宽为的小路,这块草地的绿地面积为 . 14. 如果单项式与能合并成一个单项式,那么 , .15. 已知:如图,点D是射线AB上一动点,连接CD,过点D作交直线AC于点E,若 , , 则的度数为 .
14. 如果单项式与能合并成一个单项式,那么 , .15. 已知:如图,点D是射线AB上一动点,连接CD,过点D作交直线AC于点E,若 , , 则的度数为 . 16. 数学课上,老师出示关于x,y的方程组 , 让学生以小组形式展开讨论.展示环节有下列结论:①当时,方程组的解是;②当x,y的值互为相反数时,;③不存在一个实数a使得;④若 , 则 . 上述结论中正确的个数有个.
16. 数学课上,老师出示关于x,y的方程组 , 让学生以小组形式展开讨论.展示环节有下列结论:①当时,方程组的解是;②当x,y的值互为相反数时,;③不存在一个实数a使得;④若 , 则 . 上述结论中正确的个数有个.三、解答题(本题有8小题,共66分)
-
17. 解方程组(1)、(2)、18. 如图,在正方形网格中,每个小正方形的边长都为1,三角形的顶点,点都在正方形网格的格点上.
 (1)、平移三角形 , 使点A与重合,画出平移后得到的三角形;(2)、连接 , , 则线段与的关系是;(3)、四边形的面积是(平方单位).19. 已知:如图, , , 试说明:(请按图填空,并补充理由):
(1)、平移三角形 , 使点A与重合,画出平移后得到的三角形;(2)、连接 , , 则线段与的关系是;(3)、四边形的面积是(平方单位).19. 已知:如图, , , 试说明:(请按图填空,并补充理由):
证明:(已知),
▲ ▲ , ( )
, (两直线平行,内错角相等)
又(已知)
▲ , (等量代换)
▲ ▲ , (内错角相等,两直线平行)
. ( )
20. 我们定义一个新运算,规定: , 例如: . 若 , , 分别求出x和y的值.21. 如图, , .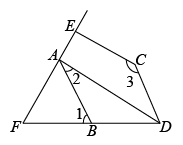 (1)、与平行吗?试说明理由;(2)、若平分 , 于点 , , 求的度数.22. 某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
(1)、与平行吗?试说明理由;(2)、若平分 , 于点 , , 求的度数.22. 某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计). (1)、若该厂购进正方形纸板1500张,长方形纸板3000张,问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;(2)、该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板80张,长方形纸板a张,全部加工成上述两种纸盒,且 , 试求在这一天加工两种纸盒时,a的所有可能值.23. 综合与实践
(1)、若该厂购进正方形纸板1500张,长方形纸板3000张,问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;(2)、该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板80张,长方形纸板a张,全部加工成上述两种纸盒,且 , 试求在这一天加工两种纸盒时,a的所有可能值.23. 综合与实践问题情境:小明同学在学习二元一次方程组时遇到了这样一个问题:
解方程组: .
(1)、观察发现:如果用代入消元法或加减消元法求解,运算量比较大,容易出错.如果把方程组中的看成一个整体,把看成一个整体,通过换元,可以解决问题.设 , , 则原方程组可化为 , 解关于m,n的方程组,得 ,
所以 , 解方程组,得 .
(2)、探索猜想:运用上述方法解下列方程组: .(3)、拓展延伸:已知关于x,y的二元一次方程组的解为 , 求关于x,y的方程组的解.24. 钱塘江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°. (1)、求a、b的值;(2)、若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)、如图,两灯同时转动,在灯A射线到达AN之前,若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
(1)、求a、b的值;(2)、若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)、如图,两灯同时转动,在灯A射线到达AN之前,若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.