浙江省金华市2023-2024学年七年级下学期第一次月考数学试题

试卷更新日期：2024-04-12 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列方程中，为二元一次方程的是（）

A、2x＋3＝0 B、3x－y＝2z C、x²＝3 D、2x－y＝5

查看试题解析
2. 如图，在下列四组条件中，能判断 $A B ∥ C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ A B D = ∠ B D C$ C、 $∠ 3 = ∠ 4$ D、 $∠ B A D + ∠ A B C = 180 °$

查看试题解析
3. 若关于x ， y的方程组 ${\begin{array}{l} 3 m x - y = n \\ 2 x + n y = m \end{array}$ 的解为 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ 则 $(m - n)^{2}$ 等于（）

A、1 B、4 C、9 D、25

查看试题解析
4. 一副三角板按图示摆放，点E恰好落在CB的延长线上，使FD∥BC ，则∠BDE的大小为（）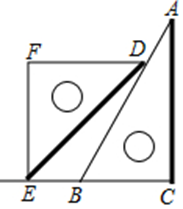

A、10° B、15° C、25° D、30°

查看试题解析
5. 兔年来临，小兰要做玩偶兔子和福袋作为新年礼物，她去市场买了36米布，每米布可以做兔子25只，或者福袋40个，小兰将1只玩偶兔子和2个福袋配成一套礼物，结果发现布没有剩余，恰好配套做成了礼物．若设用x米布做兔子，用y米布做福袋，则可列出方程组为（）

A、 ${\begin{array}{l} x + y = 36 \\ y = 2 x \end{array}$ B、 ${\begin{array}{l} x + y = 36 \\ 25 x = 2 \times 40 y \end{array}$ C、 ${\begin{array}{l} x + y = 36 \\ 25 x = \frac{40 y}{2} \end{array}$ D、 ${\begin{array}{l} x + y = 36 \\ \frac{2 x}{25} = \frac{y}{40} \end{array}$

查看试题解析
6. 二元一次方程 $2 x + y = 9$ 的正整数解有（）

A、一组 B、二组 C、三组 D、四组

查看试题解析
7. 计算 $x^{3} \cdot y^{2} \cdot (- x y^{3})^{2}$ 的结果是（）

A、 $x^{5} \cdot y^{10}$ B、 $x^{5} \cdot y^{8}$ C、 $- x^{5} \cdot y^{8}$ D、 $x^{6} \cdot y^{12}$

查看试题解析
8. 如图，直线 $M N ∥ P Q$ ， $M N$ 与直线 $A B$ 、 $A C$ 分别交于 $D$ ， $E$ ， $P Q$ 与直线 $A B$ ， $A C$ 分别交于 $F$ ， $G$ ，若 $∠ C = 75 °$ ， $∠ B G F = 26 °$ ，则 $∠ A E N$ 的度数为（）．

A、115° B、126° C、131° D、154°

查看试题解析
9. 关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x + 2 a y = 3 - a \\ - a x - 2 y = 1 \end{array}$ ， ①当 $a = 2$ 时，方程组的解是 ${\begin{array}{l} x = - 1 \\ y = \frac{1}{2} \end{array}$ ， ②当 $a = 3$ 时， $x + 2 y = \frac{1}{2}$ ；③若该方程组无解，则 $a = \pm 1$ ，以上结论中正确的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 如图，直线 $E F$ 上有两点A、C ，分别引两条射线 $A B$ 、 $C D$ ． $∠ B A F = 100 °$ ， $C D$ 与 $A B$ 在直线 $E F$ 异侧．若 $∠ D C F = 60 °$ ，射线 $A B$ 、 $C D$ 分别绕A点，C点以1度/秒和6度/秒的速度同时顺时针转动，设时间为t秒，在射线 $C D$ 转动一周的时间内，当时间t的值为何时， $C D$ 与 $A B$ 平行（）

A、4或10秒 B、10或20秒 C、10或 40秒 D、4或40秒

查看试题解析

二、填空题（每小题4分，共24分）

11. 如图， $∠ 1$ 与 $∠ 2$ 同位角．（填“是”或“不是”）

查看试题解析
12. 已知x，y满足方程组 ${\begin{array}{l} 2 x + 3 y = 3 \\ 3 x + 2 y = 7 \end{array}$ ，则2023+x+y＝．

查看试题解析
13. 已知 $x^{n} = 3$ ， $y^{n} = 2$ ，则 $(x y)^{3 n} =$ .

查看试题解析
14. 如图，△ABC的边BC长为4 cm.将△ABC平移2 cm得到△A'B'C'，且 BB'⊥BC，则阴影部分的面积为cm².

查看试题解析
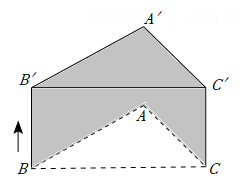15. 已知关于x，y的二元一次方程组 ${\begin{array}{l} 3 x + y = 2 k \\ x - 2 y = k + 6 \end{array}$ 有下列说法：①当x与y相等时，解得 $k = - 4$ ；②当x与y互为相反数时，解得 $k = 3$ ；③若 $4^{x} \cdot 8^{y} = 32$ ，则 $k = 11$ ；④无论k为何值，x与y的值一定满足关系式 $x + 5 y + 12 = 0$ ，其中正确的序号是．

查看试题解析
16. 图1是一盏可折叠台灯．图2，图3是其平面示意图，支架AB ， BC为固定支撑杆，支架OC可绕点C旋转调节．已知灯体顶角∠DOE＝48°，顶角平分线OP始终与OC垂直．当支架OC旋转至水平位置时（如图2），OD恰好与BC平行，则支架BC与水平方向的夹角∠θ＝°；若将图2中的OC继续向上旋转10°（如图3），则此时OD与水平方向的夹角∠DQM＝°.

查看试题解析

三、解答题

17. 解方程：

(1)、 ${\begin{array}{l} y = 2 x - 1 \\ x + 2 y = - 7 \end{array}$

(2)、 ${\begin{array}{l} 2 x + 3 y = 10 \\ 3 x + 2 y = 15 \end{array}$

查看试题解析
18. 计算

(1)、 $x^{7} \cdot x^{5} + {(- 2 x^{3})}^{4}$

(2)、 ${(b - a)}^{2} \cdot {(a - b)}^{3} + 2 {(a - b)}^{5}$

查看试题解析
19. 补全证明过程，并在括号内填写推理的依据．
已知：如图，直线a ， b ， c 被直线d ， e 所截， $∠ 1 = ∠ 2 ， ∠ 4 + ∠ 5 = 180 °$
求证： $∠ 6 = ∠ 7$ ．
证明：∵ $∠ 1 = ∠ 2$ ，
$∠ 2 = ∠ 3$ （     ）
$∴ ∠ 1 = ∠ 3$
∴    ▲         $∥ a$ （     ）
∵ $∠ 4 + ∠ 5 = 180 °$ ，
∴    ▲         $∥ b$ （     ）
∴ $a ∥ b$ ，
∴ $∠ 6 = ∠ 7$ （     ）

查看试题解析
20. 如图，在每个小正方形的边长均为1的方格纸中， $△ A B C$ 的顶点都在方格纸的格点上．

(1)、将 $△ A B C$ 平移后得到 $△ A^{'} B^{'} C^{'}$ ，图中标出了点 $B$ 的对应点 $B^{'}$ ，请补全 $△ A^{'} B^{'} C^{'}$ ；

(2)、连接 $A A^{'}$ 、 $B B^{'}$ ，则这两条线段之间的关系是；

(3)、点 $P$ 为格点，且 $S_{△ P B C} = S_{△ A B C}$ （点 $P$ 与点 $A$ 不重合），满足这样条件的 $P$ 点有个．

查看试题解析
21. 如图，已知 $∠ A = ∠ C$ ， $A D ⊥ B E$ 于点 $F$ ， $B C ⊥ B E$ 于点 $B$ ，点 $E$ ， $D$ ， $C$ 在同一条直线上．

(1)、求证： $A B ∥ C D$ ；

(2)、若 $∠ A B C = 120 °$ ，求 $∠ B E C$ 的度数．

查看试题解析
22. 甲、乙两个学校乐团，决定向某服装厂购买同样的演出服，下是服装厂给出的演出服装的价格表：
购买服装的套数
1~39套（含39套）
40~69套（含69套）
70套及以上
每套服装的价格
80元
70元
60元
经调查：两个乐团共88人（甲乐团人数不少于49人），如果分别各自购买演出服，两个乐团共需花费6500元．请回答以下问题：

(1)、如果甲、乙两个乐团联合起来购买服装，那么比各自购买服装最多可以节省多少元？

(2)、甲、乙两个乐团各有多少名学生？

(3)、现从甲乐团抽调 $a$ 人，从乙乐团抽调 $b$ 人（要求从每个乐团抽调的人数不少于5人），去儿童福利院献爱心演出，并在演出后每位乐团成员向儿童们进行“心连心活动”；甲乐团每位成员负责5位小朋友，乙乐团每位成员负责4位小朋友，这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖，请写出所有的抽调方案，并说明理由．

查看试题解析
23. 如图，直线MN//PQ，将一副三角板中的两块直角三角板如图1放置，∠ACB＝∠EDF＝90°，∠ABC＝∠BAC＝45°，∠DFE＝30°，∠DEF＝60°，此时点A与点E重合.

(1)、对于图1，固定△ABC的位置不变，将△DEF绕点E按顺时针方向进行旋转，旋转至DE与BC首次平行，如图2所示，求此时∠FAC的度数.

(2)、对于图1，固定△ABC的位置不变，将△DEF沿AC方向平移至点F正好落在直线MN上，再将△DEF绕点F按顺时针方向进行旋转，如图3所示.
①若边EF与边BC交于点G，试判断∠BGF﹣∠EFN的值是否为定值，若是定值，则求出该定值，若不是定值，请说明理由；
②对于图3，固定△ABC的位置不变，将△DEF绕点F顺时针方向以每秒10°的速度进行旋转，当EF与直线MN首次重合时停止运动当经过t秒时，线段DE与△ABC的一条边平行，求满足条件的t的值.

查看试题解析

购买服装的套数	1~39套（含39套）	40~69套（含69套）	70套及以上
每套服装的价格	80元	70元	60元