湖北省孝感市2024年中考一模数学试题

试卷更新日期：2024-04-12 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中只有一个正确选项，请在答题卡上把正确答案的代号涂黑）

1. 下列四个数中，最小的是（）

A、－2 B、 $- \frac{1}{2}$ C、2 D、 $\frac{1}{2}$

查看试题解析
2. 我国古代典籍《周易》中的“八卦”思想对我国建筑有一定的影响．如图是受“八卦”的启示，创作的正八边形窗户平面图，则对该图的对称性表述正确的是（）

A、只是轴对称图形 B、只是中心对称图形 C、既是轴对称图形，又是中心对称图形 D、既不是轴对称图形，又不是中心对称图形

查看试题解析
3. 1月9日，中国国家铁路集团有限公司发布数据称，2023年全年，国家铁路完成旅客发送量36.8亿人次，高峰日发送旅客突破2000万人次，全年和高峰日旅客发送量均创历史新高，其中数据“36.8亿”用科学记数法表示为（）

A、 $3.68 \times 1 0^{9}$ B、 $36.8 \times 1 0^{9}$ C、 $3.68 \times 1 0^{10}$ D、 $0.368 \times 1 0^{10}$

查看试题解析
4. 如图是一个由5个相同的小正方体组成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列运算中正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{2} - 2 a^{2} = - a^{2}$ C、 $a^{8} \div a^{4} = a^{2}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
6. 下列说法正确的是（）

A、成语“刻舟求剑”描述的是必然事件 B、了解央视春晚的收视率适合用抽样调查 C、调查某品牌烟花的合格率适合用全面调查 D、如果某彩票的中奖率是1%，那么一次购买100张彩票一定会中奖

查看试题解析
7. 如图，将一个等腰直角三角形放在两条平行线上，若∠1＝50°，则∠2的度数为（）

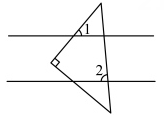A、75° B、80° C、85° D、90°

查看试题解析
8. 反比例函数 $y = \frac{k}{x}$ 的图象经过点（3，－1），则下列说法错误的是（）

A、k＝－3 B、函数图象分布在第二、四象限 C、函数图象关于原点中心对称 D、当 $x < 0$ 时，y随x的增大而减小

查看试题解析
9. 如图，AB是⊙O的弦，半径OC⊥AB ， D为圆周上一点，若∠ADC的度数为35°，则∠ABO的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
10. 如图所示，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象的对称轴是直线x＝1，且经过点（0，2）．有下列结论：① $a b c > 0$ ；② $a + b \geq m (a m + b)$ （m为常数）；③若 $(2, y_{1})$ ， $(\frac{1}{2}, y_{2})$ ， $(- 2, y_{3})$ 在该函数图象上，则 $y_{3} < y_{1} < y_{2}$ ；④ $- \frac{2}{3} < a < - \frac{1}{4}$ ．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共5小题，每小题3分，满分15分．请把答案填在答题卡相应题号的横线上）

11. 若 $\sqrt{a} > 202 4^{0}$ ，则正整数a可以为．

查看试题解析
12. 若一元二次方程 $x^{2} - 2 x - 1 = 0$ 的两个实数根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2}$ 的值为．

查看试题解析
13. 如图，电路上有①、②、③3个开关和一个小灯泡，若任意闭合电路上2个开关，则小灯泡发光的概率为．

查看试题解析
14. 小明学习相交直线时发现：3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，（1）5条直线两两相交最多有个交点；（2）n条直线两两相交最多有个交点．（用含有字母n的式子表示， $n \geq 3$ ）

查看试题解析
15. 如图，平行四边形ABCD中，AB＝4， $B C = \sqrt{37}$ ， ∠ABC＝120°，点E在AD上，将△ABE沿BE折叠得到 $△ A^{'} B E$ ，若点 $A^{'}$ 恰好在线段CE上，则AE的长为．

查看试题解析

三、解答题（本大题共9小题，满分75分，请认真读题，冷静思考，解答题应写出必要的文字说明、证明过程或演算步骤，请把解题过程写在答题卡相应题号的位置）

16. 先化简，再求值： $(m + 2 - \frac{5}{m - 2}) \div \frac{2 m - 6}{m - 2}$ ，其中 $m = - 3 + 2 \sqrt{2}$ ．

查看试题解析
17. 如图，在□ABCD中，对角线AC ， BD相交于点O ，且OA＝OB＝5，AB＝6，求□ABCD的面积．

查看试题解析
18. “阅读陪伴成长，书香润泽人生”．启智学校本学期准备开展学生阅读活动，并计划网购甲、乙两种图书．已知甲种图书每本的价格比乙种图书每本的价格多5元，购买150本甲种图书和200本乙种图书共需6000元．求甲、乙两种图书每本的价格各是多少元？

查看试题解析
19. “感受数学魅力，提升数学素养”，思远中学在校开展了数学文化知识竞赛，现从七年级和八年级参加竞赛的学生中各随机抽取了10名学生的成绩进行整理、描述和分析（单位：分，满分100分，成绩均不低于70分，90分及90分以上为优秀），并将学生竞赛成绩分为A ， B ， C三个等级：A：70≤x＜80，B：80≤x＜90，C：90≤x＜100．
下面给出了部分信息：
抽取的七年级10名学生的竞赛成绩为：75，76，84，84，84，86，86，94，95，96；
抽取的八年级10名学生的竞赛成绩在B等级的为：81，83，84，88，88．
两个年级抽取的学生成绩的平均数、中位数、众数如下表所示：
学生
平均数
中位数
众数
七年级
86
85
b
八年级
86
a
88
抽取的八年级学生竞赛成绩扇形统计图：
根据以上信息，解答下列问题：

(1)、填空：a＝， b＝， $β =$ ；

(2)、根据以上数据，请你对七年级竞赛成绩作出分析？（写一条即可）；

(3)、若八年级共有300名学生参赛，请你估计八年级参赛学生中成绩为优秀的人数．

查看试题解析
20. 如图①是某款智能磁吸键盘，如图②是平板电脑吸附在该款设备上时的照片，图③是图②的示意图．已知BC＝8cm，CD＝20cm，∠BCD＝63°．当AE与BC形成的∠ABC为116°时，求DE的长．（结果取整数）（参考数据： $s i n 63 ° \approx 0.90$ ， $c o s 63 ° \approx 0.45$ ， $t a n 63 ° \approx 1.96$ ； $s i n 53 ° \approx 0.80$ ， $c o s 53 ° \approx 0.60$ ， $t a n 53 ° \approx 1.33$ ）

查看试题解析
21. 如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A、D的⊙O分别交边AB、AC于点E、F.

(1)、求证：BC是⊙O的切线；

(2)、若 $B E = 4$ ， $s i n B = \frac{1}{2}$ ，求阴影部分的面积.

查看试题解析
22. 网络直播带货已成为一种新业态，某网店尝试用60天的时间，按单价随天数而变化的直播带货模式销售一种成本为10元/每件的商品，经过统计得到此商品的日销售量m（件）、销售单价n（元/件）在第x天（x为正整数）销售的相关信息：
①m与x满足一次函数关系，且第1天的日销售量为98件，第4天的日销售量为92件；
②n与x的函数关系如下图所示；

(1)、第5天的日销售量件；n与x的函数关系式为．

(2)、在这60天中，网店哪天销售该商品的日利润y最大？最大是多少元？

(3)、在这60天中，共有多少天日利润y不低于2418元？

查看试题解析
23. 【问题情境】如图，在△ABC中，∠ACB＝90°，AC＝kBC ， CD是AB边上的高，点E是DB上一点，连接CE ，过点A作AF⊥CE于F ，交CD于点G ．

(1)、【特例证明】如图1，当k＝1时，求证：DG＝DE；

(2)、【类比探究】如图2，当 $k \neq 1$ 时，（1）中的结论是否还成立？若成立，请写出证明过程，若不成立，请指出此时DG与DE的数量关系，并说明理由；

(3)、【拓展运用】如图3，连接DF ，若 $k = \frac{3}{4}$ ， AC＝AE ， DG＝3，求DF的长．

查看试题解析
24. 如图1，已知抛物线 $y = a x^{2} + b x + 3$ 与x轴交于点A（－1，0），B（3，0），与y轴交于点C ，连接BC ．

(1)、求a ， b的值及直线BC的解析式；

(2)、如图1，点P是抛物线上位于直线BC上方的一点，连接AP交BC于点E ，过P作PF⊥x轴于点F ，交BC于点G ，
（ⅰ）若EP＝EG ，求点P的坐标，
（ⅱ）连接CP ， CA ，记△PCE的面积为 $S_{1}$ ， △ACE的面积为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的最大值；

(3)、如图2，将抛物线位于x轴下方面的部分不变，位于x轴上方面的部分关于x轴对称，得到新的图形，将直线BC向下平移n个单位，得到直线l ，若直线l与新的图形有四个不同交点，请直接写出n的取值范围．

查看试题解析

学生	平均数	中位数	众数
七年级	86	85	b
八年级	86	a	88