湖北省十堰市郧西县2023-2024学年九年级下学期期中数学试题
试卷更新日期:2024-04-12 类型:期中考试
一、选择题(本大题10 小题,每小题3分,共30分)
-
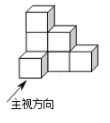
1. 若a与-2互为相反数,则a的值是( )A、-2 B、 C、 D、22. 由七个相同的小立方块搭成的几何体如图所示,则它的主视图是( )
 A、
A、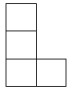 B、
B、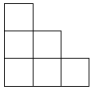 C、
C、 D、
D、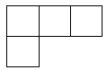 3. 把不等式组的解集表示在数轴上,下列选项正确的是( )A、
3. 把不等式组的解集表示在数轴上,下列选项正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 一块三角板和一根直尺的位置如图所示,若 , 则的度数为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 一块三角板和一根直尺的位置如图所示,若 , 则的度数为( ) A、 B、 C、 D、6. 已知点在反比例函数的图像上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、7. 今年2月,某班准备从《在希望的田野上》《我和我的祖国》《十送红军》三首歌曲中选择两首进行排练,参加永州市即将举办的“唱响新时代,筑梦新征程”合唱选拔赛,那么该班恰好选中前面两首歌曲的概率是( )A、 B、 C、 D、18. 一配电房示意图如图所示,它是一个轴对称图形,已知 , , 则房顶A离地面的高度为( )
A、 B、 C、 D、6. 已知点在反比例函数的图像上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、7. 今年2月,某班准备从《在希望的田野上》《我和我的祖国》《十送红军》三首歌曲中选择两首进行排练,参加永州市即将举办的“唱响新时代,筑梦新征程”合唱选拔赛,那么该班恰好选中前面两首歌曲的概率是( )A、 B、 C、 D、18. 一配电房示意图如图所示,它是一个轴对称图形,已知 , , 则房顶A离地面的高度为( )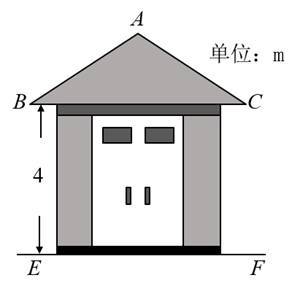 A、 B、 C、 D、9. 如图,⊙O的弦CD交直径AB于E,OD=DE,CE:DE=3:5,若OE=5,则CD的长为( )
A、 B、 C、 D、9. 如图,⊙O的弦CD交直径AB于E,OD=DE,CE:DE=3:5,若OE=5,则CD的长为( )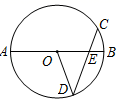 A、4 B、4 C、3 D、310. 抛物线的图象如图所示,对称轴为直线. 下列说法:①;②; ③(为全体实数);④若图象上存在点 , , 当时,满足 , 则m的取值范围为 , 其中正确的个数有( )
A、4 B、4 C、3 D、310. 抛物线的图象如图所示,对称轴为直线. 下列说法:①;②; ③(为全体实数);④若图象上存在点 , , 当时,满足 , 则m的取值范围为 , 其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题10 小题,每小题3分,共30分)
-
11. 化简:的结果为 .12. 若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .13. 若正n边形的一个外角等于 , 那么 .14. 我国明代数学读本《算法统宗》中有一道题, 其题意为:客人一起分银子,若每人两, 还剩两;若每人两,还差两; 则人数为 人;银子共有两.15. 如图,在平面直角坐标中,矩形的边 , , 将矩形沿直线折叠到如图所示的位置, 线段恰好经过点B , 点 C落在y轴的点位置,点 E 的坐标是 .

三、解答题
-
16. 计算:17. 如图,矩形中,过对角线的中点O作的垂线 , 分别交 , 于点E , F;连接、 . 求证:四边形是菱形.
 18. 随着我国科技事业的不断发展,国产无人机大量进入快递行业.现有A,B两种型号的无人机都被用来运送快件,A型机比B型机平均每小时多运送20件,A型机运送700件所用时间与B型机运送500件所用时间相等,两种无人机平均每小时分别运送多少快件?19. 近年,“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了两幅不完整的统计图.请根据图中信息解答下列问题:
18. 随着我国科技事业的不断发展,国产无人机大量进入快递行业.现有A,B两种型号的无人机都被用来运送快件,A型机比B型机平均每小时多运送20件,A型机运送700件所用时间与B型机运送500件所用时间相等,两种无人机平均每小时分别运送多少快件?19. 近年,“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了两幅不完整的统计图.请根据图中信息解答下列问题: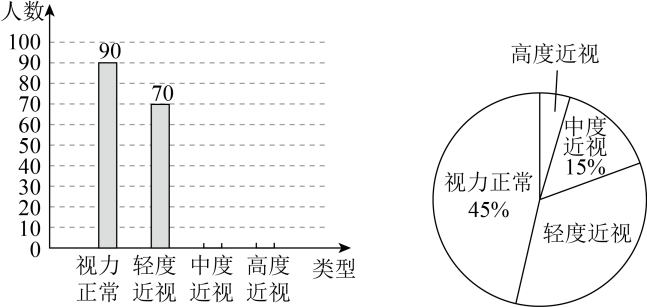 (1)、所抽取的学生人数为;(2)、补全条形统计图,并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数;(3)、该校共有学生人,请估计该校学生中近视程度为“轻度近视”的人数.20. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 与反比例函数在第四象限内的图象交于点 .
(1)、所抽取的学生人数为;(2)、补全条形统计图,并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数;(3)、该校共有学生人,请估计该校学生中近视程度为“轻度近视”的人数.20. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 与反比例函数在第四象限内的图象交于点 . (1)、求一次函数和反比例函数的表达式:(2)、当时,直接写出的取值范围.21. 如图,中,以为直径的交于点E.平分 , 过点E作于点D,延长交的延长线于点P.
(1)、求一次函数和反比例函数的表达式:(2)、当时,直接写出的取值范围.21. 如图,中,以为直径的交于点E.平分 , 过点E作于点D,延长交的延长线于点P.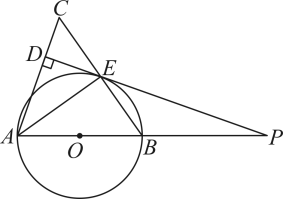 (1)、求证:是的切线;(2)、若 , 求的长.22. 某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.(1)、求该产品第一年的利润w(万元)与售价x之间的函数关系式;(2)、该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?
(1)、求证:是的切线;(2)、若 , 求的长.22. 某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.(1)、求该产品第一年的利润w(万元)与售价x之间的函数关系式;(2)、该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?