2024年浙教版数学八年级下册阶段复习培优练第1-6章
试卷更新日期:2024-04-10 类型:复习试卷
一、选择题
-
1. 菱形具有而矩形不一定具有的性质是( )A、对边平行 B、对角线互相平分 C、对角线互相垂直 D、对角互补2. 如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
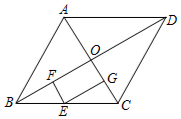 A、 B、 C、 D、3. 如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.若∠DAC=20°,∠ACB=66°,则∠FEG的度数为( )
A、 B、 C、 D、3. 如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.若∠DAC=20°,∠ACB=66°,则∠FEG的度数为( ) A、18° B、21° C、22° D、23°4. 如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD ,AB的对称点为E1 , E2;点F关于BC,CD的对称点为F1 , F2 , 在整个过程中,四边形E1E2F1F2形状的变化依次是( )
A、18° B、21° C、22° D、23°4. 如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD ,AB的对称点为E1 , E2;点F关于BC,CD的对称点为F1 , F2 , 在整个过程中,四边形E1E2F1F2形状的变化依次是( ) A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形5. 如图,在中, , D、E分别为、的中点,平分 , 交于点F,若 , , 则的长为( )
A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形5. 如图,在中, , D、E分别为、的中点,平分 , 交于点F,若 , , 则的长为( ) A、2 B、1 C、4 D、6. 如图,已知点 , 点M,N分别是直线和直线上的动点,连接 , . 的最小值为( )
A、2 B、1 C、4 D、6. 如图,已知点 , 点M,N分别是直线和直线上的动点,连接 , . 的最小值为( )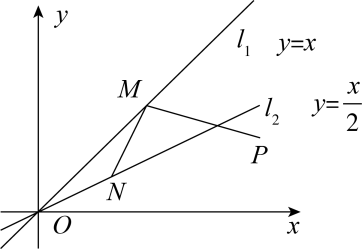 A、2 B、 C、 D、7. 如图,正方形的边长为 , 点和点在轴正半轴上,点、在第一象限,一次函数的图象交、分别于、 . 若与的面积比为 , 则的值为( )
A、2 B、 C、 D、7. 如图,正方形的边长为 , 点和点在轴正半轴上,点、在第一象限,一次函数的图象交、分别于、 . 若与的面积比为 , 则的值为( )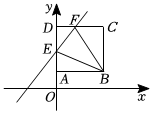 A、 B、 C、 D、8. 如图,直线分别与x轴、y轴交于点A、B,点C在线段上,线段沿翻折.点O落在边上的点D处.以下结论:①;②直线的解析式为;③点;④若线段上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的横坐标是 . 以上所有结论中正确的个数是( )
A、 B、 C、 D、8. 如图,直线分别与x轴、y轴交于点A、B,点C在线段上,线段沿翻折.点O落在边上的点D处.以下结论:①;②直线的解析式为;③点;④若线段上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的横坐标是 . 以上所有结论中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 在边长为4的正方形ABCD中,连结对角线AC,BD,点P是正方形边上或对角线上的一点,若PB=3PC,则PC= .10. 如图,在平面直角坐标系中,□CODE的顶点C 在x轴的负半轴上,点D,E在第二象限,点E的纵坐标为2,反比例函数 的图象与OD 相交于点A(a,b).若点 B的坐标为 且点B 在∠ODE的边上,则 OB 的长.为.
 11. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 .
11. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 . 12. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 .
12. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 .
三、综合题
-
13. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
 (1)、求证:四边形ADFE是矩形;(2)、连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.14. 2023年3月5日,中华人民共和国第十四届全国人民代表大会第一次会议在北京召开,某校为使学生更好地了解“两会”,争做新时代好少年,开展了“两会”知识竞赛活动,分别从八(1)班和八(2)班各随机抽取10名学生的竞赛成绩(单位:分,满分100分),并对数据进行了如下分析与整理:
(1)、求证:四边形ADFE是矩形;(2)、连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.14. 2023年3月5日,中华人民共和国第十四届全国人民代表大会第一次会议在北京召开,某校为使学生更好地了解“两会”,争做新时代好少年,开展了“两会”知识竞赛活动,分别从八(1)班和八(2)班各随机抽取10名学生的竞赛成绩(单位:分,满分100分),并对数据进行了如下分析与整理:收集数据
八(1)班学生知识竞赛成绩:84,75,82,70,91,83,80,74,79,82
八(2)班学生知识竞赛成绩:80,65,75,68,95,82,84,80,92,79
分析数据
平均数/分
中位数/分
众数/分
方差
八(1)班
80
b
82
31.6
八(2)班
a
80
c
78.4
根据以上信息,解答下列问题:
(1)、填空: , , .(2)、请你对八(1)班和八(2)班抽取的这10名学生的知识竞赛成绩作出评价.(3)、该校除开展两会知识竞赛活动外,还组织了制作关于“两会”手抄报的评比活动,并对手抄报进行评分(单位:分,满分100分).在八(2)班抽取的这10名学生中,甲同学和乙同学的知识竞赛成绩分别为95分和92分,手抄报成绩分别为70分和80分.现对甲同学和乙同学进行综合评分,若知识竞赛成绩占70%,手抄报成绩占30%,则哪位同学的综合成绩较好?15. 如图,直线:分别交轴,轴于两点, . (1)、直接写出的值为;(2)、如图1,直线与分别交轴于点 , 将线段平移后的对应线段(点的对应点为 , 点的对应点为)的两个端点恰好落在两条直线上,若四边形为菱形,求的值;(3)、如图2,点在直线上,点 , 以为边在右侧作正方形 , 连接 , 求的最小值.
(1)、直接写出的值为;(2)、如图1,直线与分别交轴于点 , 将线段平移后的对应线段(点的对应点为 , 点的对应点为)的两个端点恰好落在两条直线上,若四边形为菱形,求的值;(3)、如图2,点在直线上,点 , 以为边在右侧作正方形 , 连接 , 求的最小值.