2024年浙教版数学八年级下册阶段复习提高练第1-6章
试卷更新日期:2024-04-10 类型:复习试卷
一、选择题
-
1. 的三边长a , b , c满足 , 则是( )A、等腰直角三角形 B、等腰三角形 C、直角三角形 D、等边三角形2. 如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )
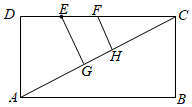 A、 B、 C、3 D、3. 如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A、 B、 C、3 D、3. 如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )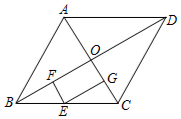 A、 B、 C、 D、4. 如图,已知菱形的边与轴重合,点 , , B(-3,0)若固定点 , , 将菱形沿箭头方向推,当点落在轴上时,点的坐标为( )
A、 B、 C、 D、4. 如图,已知菱形的边与轴重合,点 , , B(-3,0)若固定点 , , 将菱形沿箭头方向推,当点落在轴上时,点的坐标为( ) A、 B、 C、 D、5. 如图,在矩形中,对角线、相交于点 , 于点 , :: , 且 , 则的长度是( )
A、 B、 C、 D、5. 如图,在矩形中,对角线、相交于点 , 于点 , :: , 且 , 则的长度是( ) A、 B、 C、 D、6. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
A、 B、 C、 D、6. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( ) A、1 B、 C、 D、7. 如图是反比例函数 的图象,点 A(x,y)是反比例函数图象上任意一点,过点 A 作 AB⊥x轴于点B,连结OA,则△AOB的面积是 ( )
A、1 B、 C、 D、7. 如图是反比例函数 的图象,点 A(x,y)是反比例函数图象上任意一点,过点 A 作 AB⊥x轴于点B,连结OA,则△AOB的面积是 ( ) A、 B、1 C、 D、28. 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,则下列结论一定正确的是( )
A、 B、1 C、 D、28. 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,则下列结论一定正确的是( ) A、四边形EFGH是矩形 B、四边形EFGH的内角和小于四边形ABCD的内角和 C、四边形EFGH的周长等于四边形ABCD的对角线长度之和 D、四边形EFGH的面积等于四边形ABCD的面积的
A、四边形EFGH是矩形 B、四边形EFGH的内角和小于四边形ABCD的内角和 C、四边形EFGH的周长等于四边形ABCD的对角线长度之和 D、四边形EFGH的面积等于四边形ABCD的面积的二、填空题
-
9. 如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为
 10. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1 , k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是
10. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1 , k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是 11. 某超市经销的洗衣液中,甲、乙两个品牌比较畅销,其中甲品牌洗衣液的进价为30元/瓶,乙品牌洗衣液的进价每瓶比甲品牌高10元.在销售中,该超市发现,若将甲品牌的洗衣液以每瓶45元出售,则每天固定售出100瓶,而乙品牌的洗衣液每瓶售价50元时,每天可售出140瓶,且当乙品牌的洗衣液每瓶售价每提高1元时,每天就会少售出2瓶.当乙品牌洗衣液每瓶的售价为元时,两种品牌的洗衣液每天的销售利润之和为4700元.12. 如图,菱形 ABCD的边长为 2,∠DAB=60°,E为 BC 边的中点,P 为对角线AC 上的一个动点,则 PB+PE的最小值为.
11. 某超市经销的洗衣液中,甲、乙两个品牌比较畅销,其中甲品牌洗衣液的进价为30元/瓶,乙品牌洗衣液的进价每瓶比甲品牌高10元.在销售中,该超市发现,若将甲品牌的洗衣液以每瓶45元出售,则每天固定售出100瓶,而乙品牌的洗衣液每瓶售价50元时,每天可售出140瓶,且当乙品牌的洗衣液每瓶售价每提高1元时,每天就会少售出2瓶.当乙品牌洗衣液每瓶的售价为元时,两种品牌的洗衣液每天的销售利润之和为4700元.12. 如图,菱形 ABCD的边长为 2,∠DAB=60°,E为 BC 边的中点,P 为对角线AC 上的一个动点,则 PB+PE的最小值为.
三、解答题
-
13. 2023年6月5日是第50个世界环境日,今年的主题是“减塑捡塑”,旨在提高人们对塑料污染的认识,鼓励人们减少使用一次性塑料制品.为了庆祝第50个世界环境日,学校举办环境保护知识竞赛活动,竞赛内容分“自然环境保护”,“地球生物保护”,“人类环境保护”,“生态环境保护”四个项日,下表是小亮和小彬的各项成绩:(百分制)
项目
自然环境保护
地球生物保护
人类环境保护
生态环境保护
小亮
95
90
85
90
小彬
80
90
100
90
若“自然环境保护”,“地球生物保护”,“人类环境保护”,“生态环境保护”四个项目按确定综合成绩,则小亮和小彬谁的综合成绩高?请通过计算说明理由.

