2024年浙教版数学八年级下册阶段复习培优练第1-3章

试卷更新日期：2024-04-10 类型：复习试卷

进入出卷网下载

一、选择题

1. 五名学生投篮训练，规定每人投10次，记录他们每人投中的次数，得到五个数据，经分析这五个数据的中位数为6，唯一众数是7，则他们投中次数占投篮总次数的百分率可能是（）

A、 $40 %$ B、 $56 %$ C、 $60 %$ D、 $62 %$

查看试题解析
2. 用[x]表示不大于x的最大整数，则方程 $x^{2} - 2 [x] - 3 = 0$ 的解的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
3. 已知a= $\frac{1}{\sqrt{2} + 1}$ ，b= $\frac{1}{\sqrt{2} - 1}$ ，则a与b的关系是（）

A、相等 B、互为相反数 C、互为倒数 D、平方值相等

查看试题解析
4. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A、20 B、18 C、15 D、14

查看试题解析
5. 若二次根式 $\sqrt{2 - m}$ 有意义，且关于x的分式方程 $\frac{m}{1 - x}$ +2＝ $\frac{3}{x - 1}$ 有正数解，则符合条件的整数m的和是（）

A、﹣7 B、﹣6 C、﹣5 D、﹣4

查看试题解析
6. 如图，在矩形ABCD中，点E，F在对角线AC的两侧，且到所在三角形三边的距离都等于1．若AC=5，则EF的长为（）

A、 $\frac{5}{2}$ B、 $\sqrt{5}$ C、 $\frac{12}{5}$ D、 $2 \sqrt{2}$

查看试题解析
7. 有两个一元二次方程：M：ax²＋bx＋c＝0，N：cx²＋bx＋a＝0，以下四个结论中，错误的是（）

A、如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 B、如果方程M有两根符号相同，那么方程N也有两根符号相同 C、如果5是方程M的一个根，那么 $\frac{1}{5}$ 是方程N的一个根 D、如果方程M和方程N有一个相同的实数根，那么这个根必是x＝1

查看试题解析
8. 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（）

A、平均数和中位数不变 B、平均数增加，中位数不变 C、平均数不变，中位数增加 D、平均数和中位数都增大

查看试题解析

二、填空题

9. 若实数 $a$ ， $b$ 满足 $a - 2 a b + 2 a b^{2} + 4 = 0$ ，则 $a$ 的最大值与最小值之和为．

查看试题解析
10. 已知 $x = \sqrt{3} + 1$ ， $y = \sqrt{3} - 1$ ，则代数式 $\frac{y}{x} + \frac{x}{y}$ 的值是．

查看试题解析
11. 已知 $y = \sqrt{x^{2} - 4 x + 4} - x + 3$ ，当x分别取1，2，3，…，2022时，所对应的y值的总和是．

查看试题解析
12. 对于实数a，b，定义运算“⊗”： $a \otimes b = {\begin{cases} a b - b^{2} (a \geq b) \\ a^{2} - a b (a < b) \end{cases}$ ，例如：5⊗3，因为5＞3，所以5⊗3=5×3﹣3²=6．若x₁ ， x₂是一元二次方程x²﹣6x+8=0的两个根，则x₁⊗x₂= ．

查看试题解析

三、解答题

13. [数据观念]甲、乙两运动员的射击成绩(射击成绩均为整数，且靶心为10环)统计如下表(不完全)所示：
次序
1
2
3
4
5
甲的射击成绩(环)
10
8
9
10
8
乙的射击成绩(环)
10
9
9
a
b

某同学计算出了甲的成绩的平均数是9环，
方差是 $S_{}^{2} = \frac{1}{5} [{(10 - 9)}^{2} + {(8 - 9)}^{2} + (9 - 9)^{2} + (10 - 9)^{2} + (8 - 9)^{2}] = 0.8$ (环²).请回答下列问题：

(1)、在图中用折线将甲的成绩表示出来.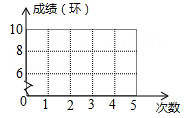

(2)、若甲、乙射击成绩的平均数都一样，则a+b=.

(3)、在(2)的条件下，当甲比乙的成绩稳定时，请列举出a，b所有可能的取值，并说明理由.

查看试题解析
14. 商店里有A，B 两种糖果，A种糖果的单价为a 元/千克，B种糖果的单价为b元/千克，且a≠b.商店准备用这两种糖果混合制成若干种什锦糖，什锦糖的定价方法是：若取m千克A 种糖果和n千克B 种糖果混合制成什锦糖，则什锦糖的售价定为总价除以总质量，即 $\frac{m a + n b}{m + n}$

(1)、某种什锦糖由 A，B两种糖果按质量比1：3混合制成，求该种什锦糖的售价.

(2)、现有甲、乙两种什锦糖，均由A，B两种糖果混合制成，其中甲什锦糖由相同质量的 A，B两种糖果混合制成；乙什锦糖由相同总价的A，B两种糖果混合制成，则甲、乙两种什锦糖的售价分别为多少？

(3)、选择合适的方法比较（2）中甲、乙两种什锦糖的售价哪个更高？

查看试题解析
15. 所谓完全平方式，就是对于一个整式 $A$ ，如果存在另一个整式 $B$ ，使 $A = B^{2}$ ，那么称 $A$ 是完全平方式. 例如 $： a^{4} = {(a^{2})}^{2} ， 4 a^{2} - 4 a + 1 = (2 a - 1)^{2}$ .

(1)、下列各式中，属于完全平方式的是 (填序号).
① $a^{6}$ ；② $x^{2} + 4 x + 4 y^{2}$ ； ③ $4 a^{2} - 2 a b + \frac{1}{4} b^{2}$ ；
④ $a^{2} - a b + b^{2}$ ； ⑤ $x^{2} - 6 x + 9$ ； ⑥ $a^{2} + a - 0.25$ .

(2)、若 $4 x^{2} + 5 x y + m y^{2}$ 和 $x^{2} - n x y + \frac{1}{4} y^{2}$ 都是完全平方式(其中 $m ， n$ 都是常熟)，求 ${(m - \frac{1}{n})}^{- 1}$ 的值.

(3)、如果多项式 $16 x^{2} + 1$ 加上一个单选式后，能成为一个完全平方式，那么加上的单选式可以是哪些(请直接写出所有可能的情况)?

查看试题解析

次序	1	2	3	4	5
甲的射击成绩(环)	10	8	9	10	8
乙的射击成绩(环)	10	9	9	a	b