2024年浙教版数学八年级下册阶段复习培优练第5章特殊平行四边形

试卷更新日期：2024-04-10 类型：复习试卷

进入出卷网下载

一、选择题

1. 边长为1的正方形的对角线的长是（）

A、整数 B、分数 C、有理数 D、无理数

查看试题解析
2. 如图，已知正方形ABCD的面积为64平方厘米， $D E = 10$ 厘米，则CE的长为（）

A、6 B、12 C、 $2 \sqrt{31}$ D、 $2 \sqrt{41}$

查看试题解析
3. 如图，大正方形与小正方形的面积之差是50，则阴影部分的面积是（）

A、12.5 B、25 C、50 D、100

查看试题解析
4. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载，如图以直角三角形的各边为边分别向同侧作正方形，若知道图中阻影部分的面积之和，则一定能求出（　　）

A、正方形 $A B E D$ 的面积 B、正方形 $A C F G$ 的面积 C、正方形 $B C M N$ 的面积 D、 $△ A B C$ 的面积

查看试题解析
5. 新冠疫情防控过程中，某中学在大门口的正上方A处装着一个红外线激光测温仪，离地 $A B = 2.1$ 米（如图所示），当人体进入感应范围内时，测温仪就会显示人体体温．一个身高1.6米的学生（ $C D = 1.6$ 米）正对门缓慢走到离门1.2米的地方时（ $B C = 1.2$ 米），测温仪自动显示体温，则人头顶离测温仪的距离 $A D$ 等于（）

A、1.2米 B、1.3米 C、1.4米 D、1.5米

查看试题解析
6. “赵爽弦图”被誉为“中国数学界的图腾”，它是由四个全等的直角三角形和一个小正方形组成的大正方形，如图，连接 $A E$ ，若大正方形 $A B C D$ 的面积为 $25 ， △ A B E$ 的面积为8，则小正方形 $E F G H$ 的面积是（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、2

查看试题解析
7. 如图，四边形ABCD是正方形，直线a，b，c分别通过A、D、C三点，且a∥b∥c．若a与b之间的距离是5，b与c之间的距离是7，则正方形ABCD的面积是（　　）

A、148 B、144 C、74 D、70

查看试题解析
8. 如图，四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD，连结AC，交BE于点P，若正方形ABCD的面积为28，AE+BE＝7.则S_△_CFP﹣S_△_AEP的值是（）

A、3.5 B、4.5 C、5 D、5.5

查看试题解析

二、填空题

9. 如图，在平面直角坐标系中，长方形OABC的顶点O在坐标原点，顶点A、C分别在x、y轴的正半轴上：OA＝3，OC＝4，D为OC边的中点，E是OA边上的一个动点，当△BDE的周长最小时，E点坐标为．

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，以 $B C$ 为边向上作正方形 $B C D E$ ，以 $A C$ 为边作正方形 $A C F G$ ，点D落在 $G F$ 上，连接 $A E$ ， $E G$ ．若 $A B = \frac{9}{2}$ ， $B C + G D = 9$ ，则 $△ A E G$ 的面积为．

查看试题解析
11. 如图，长方形ABCD中，AB＝8，AD=6，长方形内有一个点P ，连接AP ， BP，CP ，已知∠APB＝90°，CP=CB，延长CP交AD于点E ，则AE＝．

查看试题解析
12. 如图，点P是矩形 $A B C D$ 内任意一点，连结 $P A ， P B ， P C ， P D$ ，记 $∠ P A B = θ_{1} ， ∠ P B C = θ_{2} ， ∠ P C D = θ_{3} ， ∠ P D A = θ_{4}$ ，则下列各结论一定成立的有（填序号）
① $S_{△ P A D} + S_{△ P B C} = S_{△ P A B} + S_{△ P C D}$ ；②若 $∠ A P B = 80 ° ， ∠ D P C = 50 °$ ，则 $θ_{1} - θ_{2} + θ_{3} - θ_{4} = 50 °$ ；
③ $P A^{2} + P C^{2} = P B^{2} + P D^{2}$ ；④ $S_{△ A B P} = S_{△ A D P}$ ，则P在对角线 $A C$ 上

查看试题解析

三、解答题

13. [推理能力]如图，在□ABCD中，AB=2cm，AC=5cm ，S▱ABCD =8 cm²，点 E 从点 B 出发，以1cm/s的速度在 AB 的延长线上向右运动，同时点 F 从点 D 出发，以同样的速度在 CD的延长线上向左运动，运动时间为t(s).

(1)、在运动过程中，四边形 AECF 的形状是 .

(2)、当t=时，四边形 AECF 是矩形.

(3)、当 t 的值为多少时，四边形 AECF 是菱形?

查看试题解析
14. 如图，在平面直角坐标系中，矩形OABC的顶点A在x轴的正半轴上，顶点C在y轴的正半轴上，OA＝12，OC＝9，连接AC．

(1)、填空：点A的坐标：；点B的坐标：．

(2)、若CD平分∠ACO，交x轴于D，求点D的坐标．

(3)、在（2）的条件下，经过点D的直线交直线BC于E，当△CDE为以CD为底的等腰三角形时，求该直线的解析式．

查看试题解析
15.

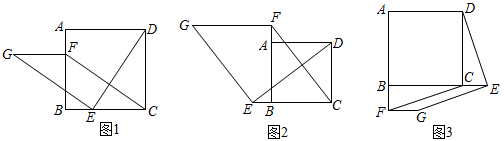(1)、问题发现：
如图1，在正方形ABCD中，点E、F分别是边BC、AD上的点，且 $C E = B F$ ，连接DE，过点E作 $E G ⊥ D E$ ，使 $E G = D E$ ，连接FG、FC，请判断：FG与CE的数量关系是，位置关系是．

(2)、拓展探究：
如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请写出判断，并给予证明．

(3)、类比延伸：
如图3，若点E、F分别是BC、AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断，不需证明．

查看试题解析