2024年浙教版数学八年级下册阶段复习培优练第4章平行四边形
试卷更新日期：2024-04-10 类型：复习试卷
一、选择题
-
1. 已知一个多边形的每个外角都等于 ， 则从这个多边形的某个顶点画对角线，可以画出几条（ ）A、5条 B、6条 C、7条 D、8条2. 用反证法证明：若a≥b>0、则a≥b2 ． 应先假设（ ）A、a<b B、a≤b C、a2<b2 D、a2≤b23. 如图是用边长相等的等边三角形和正边形两种地砖铺设的部分地面示意图，则正边形的内角和为（ ）
A、 B、 C、 D、4. 如图，点A、B、C、D、E在同一平面内，连接AB、BC、CD、DE、EA，若∠BCD=100°，则∠A+∠B+∠D+∠E＝（ ）
A、220° B、240° C、260° D、280°5. 一个三角形的三个外角之比为3：4：5，则这个三角形三个内角之比是（ ）A、5：4：3 B、3：2：1 C、4：3：2 D、5：3：16. 如图，在平面直角坐标系xOy中，已知直线AB与y轴交于点A（0，6），与x轴的负半轴交于点B ， 且∠BAO＝30°， M、N是该直线上的两个动点，且MN＝2，连接OM、ON ， 则△MON周长的最小值为 （ ）
A、2＋3 B、2＋2 C、2＋2 D、5＋7. 将一长方形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（ ）A、360° B、540° C、720° D、730°8. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°， ， 则下列结论：①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ，正确的个数是（ ）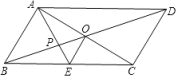
A、1 B、2 C、3 D、4二、填空题
-
9. 已知一个包装盒的底面是内角和为720°的多边形，它是由另一个多边形纸片剪掉一个角以后得到的，则原多边形是边形．10. 如图所示，△ABO与△CDO称为“对顶三角形”，其中∠A+∠B=∠C+∠D．利用这个结论，在图2中，∠A+∠B+∠C+∠D+∠E+∠F+∠G=
11. 如图，在平行四边形ABCD中，∠C=120°，AD=4，AB=2，点H、G分别是边CD、BC上的动点．连接AH、HG ， 点E为AH的中点，点F为GH的中点，连接EF则EF的最大值与最小值的差为 ．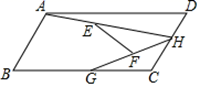
12. 如图，△ABC为等腰直角三角形，∠ABC=90°，点P在AC的延长线上，且AC=CP=4，将△ABC沿AB方向平移得到△A'B'C'，连结PA'，PC'，则△PA'C'的周长的最小值为.
三、解答题
-
13. 知识背景：
过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)、如图1，直线m 经过▱ABCD对角线的交点 O，则(填“〉”“〈”或“=”).(2)、将两个正方形按如图2 所示的方式摆放，O为小正方形对角线的交点，作过点 O 且将整个图形分成面积相等的两部分的直线.(3)、将8个大小相同的正方形按如图3 所示的方式摆放，作将整个图形分成面积相等的两部分的直线（用三种不同的方法）.14. 如图1，在△ABC中，AB＝AC，∠ABC＝ɑ，D是BC边上一点，以AD为边作△ADE，使AE＝AD，∠DAE+∠BAC＝180°．
(1)、若α＝46°，求∠ADE的度数；(2)、以AB、AE为边作平行四边形ABFE．①如图2，若点F恰好落在DE上．求证：BD＝CD；
②如图3，若点F恰好落在BC上．求证：BD＝CF．
15. 【发现与证明】如图，在四边形ABCD中，E、F、G、H是各边中点，对角线AC、BD相交于点O，I、J是AC、BD的中点，连接EF、EH、HG、GF、EI、GI、EJ、FJ、IJ、GJ、IH.
结论1：四边形EFGH是平行四边形；
结论2：四边形EJGI是平行四边形；
结论3：；
……
(1)、请选择其中一个结论，加以证明（只需证明一个结论）.
(2)、【探究与应用】（★温馨提示：以下问题可以直接使用上述结论）
①如图1，在四边形ABCD中，F、H分别为边AB，DC的中点，连结HF.已知 ， ， 线段HF的取值范围是 ▲ .
②如图2，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，连接EG，FH交于点O，cm，cm， ， 求.