2024年浙教版数学八年级下册阶段复习培优连第3章数据分析初步

试卷更新日期：2024-04-10 类型：复习试卷

进入出卷网下载

一、选择题

1. 一组由小到大排列的数据为 $- 1$ ， 0，4， $x$ ， 6，16，这组数据的中位数为5，则这组数据的众数可能是 $($ 　　 $)$

A、5 B、6 C、 $- 1$ D、5.5

查看试题解析
2. 若一组数据 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 的平均数为4，方差为3，那么数据 $a_{1} + 2$ ， $a_{2} + 2$ ， $a_{3} + 2$ 的平均数和方差分别是（）

A、4， 3 B、6 $，$ 3 C、3 $，$ 4 D、6 5

查看试题解析

3. 在一次中考体育模拟测试中，某班41名学生参加测试（满分为40分），成绩统计如下表.部分数据被遮盖，下列统计量中，与被遮盖的数据无关的是（）

成绩（分）	32	34	36	37	38	39	40
人数（人）			2	6	19		7

A、中位数、众数 B、中位数、方差 C、平均数、众数 D、平均数、方差

查看试题解析

4. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A、20 B、18 C、15 D、14

查看试题解析
5. 为响应“双减”政策，进一步落实“立德树人、五育并举”的思想主张，深圳某学校积极推进学生综合素质评价改革，小芳在本学期德、智、体、美、劳的评价得分如图所示，其各项的得分分别为9，8，10，8，7，则该同学这五项评价得分的众数，中位数，平均数分别为（）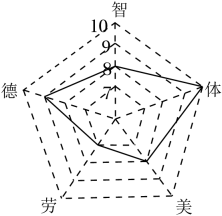

A、8，8，8 B、7，8，7.8 C、8，8，8.7 D、8，8，8.4

查看试题解析
6. 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是（）

A、平均数为10，方差为2 B、平均数为11，方差为3 C、平均数为11，方差为2 D、平均数为12，方差为4

查看试题解析
7. 每次监测考试完后，老师要对每道试题难度作分析 $.$ 已知：题目难度系数 $=$ 该题参考人数得分的平均分 $\div$ 该题的满分 $.$ 上期全市八年级期末质量监测，有 $11623$ 名学生参考 $.$ 数学选择题共设置了 $12$ 道单选题，每题 $5$ 分 $.$ 最后一道单选题的难度系数约为 $0.34$ ，学生答题情况统计如表：
选项
留空
多选
$A$
$B$
$C$
$D$
人数
$11$
$22$
$4209$
$3934$
$2057$
$1390$
占参考人数比 $(%)$
$0.09$
$0.19$
$36.21$
$33.85$
$17.7$
$11.96$
根据数据分析，可以判断本次监测数学最后一道单选题的正确答案应为（）

A、 $A$ B、 $B$ C、 $C$ D、 $D$

查看试题解析
8. 某创意工作室6位员工的月基本工资如图所示，因业务发展需要，现决定招聘一名新员工.若新员工的月基本工资为 4 500元，则下列关于现在7位员工的月基本工资的平均数和方差的说法中，正确的是（）
某创意工作室6位员工的月基本工资折线统计图

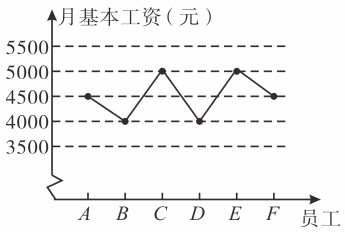A、平均数不变，方差变大 B、平均数不变，方差变小 C、平均数不变，方差不变 D、平均数变小，方差不变

查看试题解析

二、填空题

9. 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S² ，那么数据a+99，b+100，c+101的方差将 S²（填“大于”“小于”或“等于”）.

查看试题解析
10. 教练对跳远运动员小刚的训练效果进行了测试，6次跳远的成绩(单位：m)如下：7.6，7.8，7.7，7.8，8.0，7.9.这6次成绩的平均数是7.8m，方差是 $\frac{1}{60}$ m².若小刚再跳两次，成绩分别是7.7，7.9，则小刚这8次跳远成绩的方差将(填“变大”“变小”或“不变”).

查看试题解析
11. 已知：一组自然数1，2，3…k，去掉其中一个数后剩下的数的平均数为16，则去掉的数是．

查看试题解析
12. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

查看试题解析

三、解答题

13. 2022年是党和国家历史上极为重票的一年，面对风高浪急的国际环境和艰巨繁重的国内改革发展稳定任务，全国人民同心块力，顺利完成了经济保持增长，发展质量稳步提升的目标.2023年2月28日，国家统计局发布了《2022年国民经济和社会发展统计公报》，以下材料是公报中的部分内容．
材料一：如图是2018年到-2022年全年国内生产总值及其增长速度统计图．

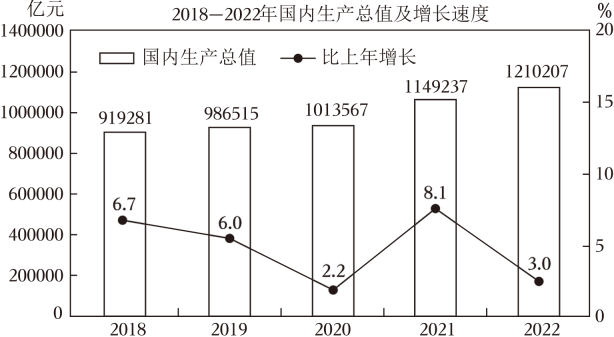
2022年是党和国家历史上极为重票的一年，面对风高浪急的国际环境和艰巨繁重的国内改革发展稳定任务，全国人民同心块力，顺利完成了经济保持增长，发展质量稳步提升的目标.2023年2月28日，国家统计局发布了《2022年国民经济和社会发展统计公报》，以下材料是公报中的部分内容．
根据以上信息回答下列问题：

(1)、从2018年到2022年，全年国内生产总值增长最快的是年，从2018年到2022年，全年国内生产总值增长率的中位数是 %．

(2)、在十四届全国人大一次会议上，李克强总理在政府工作报告中指出，2023年全年国内生产总值增长目标为5% ，请以此估计2023年全年国内生产总值．（结果精确到万亿元）

(3)、小明同学阅读了材料二，发现如果将2022年的第一、二、三产业的增长率求平均数 $\frac{4.1 % + 3.8 % + 2.3 %}{3} = 3.4 %$ ，这与2022年全年国内生产总值增长速度3.0%不符，请说明原因.

查看试题解析
14. 某中学积极推进校园文学创作，倡导每名学生每学期向校报编辑部至少投1篇稿件．学期末，学校对七、八年级的学生投稿情况进行调查．
【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生，统计每人在本学期投稿的篇数，制作了频数分布表．
投稿篇数（篇）
1
2
3
4
5
七年级频数（人）
7
10
15
12
6
八年级频数（人）
2
10
13
21
4
【数据的描述与分析】

(1)、求扇形统计图中圆心角 $α$ 的度数，并补全频数直方图．

(2)、根据频数分布表分别计算有关统计量：
统计量
中位数
众数
平均数
方差
七年级
3
3
$\bar{x}$
1.48
八年级
m
n
3.3
1.01
直接写出表格中m、n的值，并求出 $\bar{x}$ ．

(3)、【数据的应用与评价】
从中位数、众数、平均数、方差中，任选两个统计量，对七、八年级学生的投稿情况进行比较，并做出评价．

查看试题解析
15. 为了了解甲、乙、丙三种型号的扫地机器人的扫地质量，工作人员从某月生产的甲、乙、丙三种型号扫地机器人中各随机抽取10台，在完全相同条件下试验，记录下它们的除尘指数的数据，并进行整理、描述和分析，下面给出了部分信息．
ⅰ.甲、乙两种型号扫地机器人除尘指数的折线图：

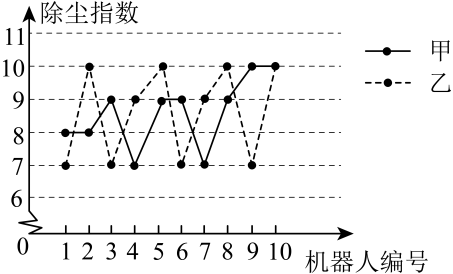
ⅱ.丙型号扫地机器人的除尘指数数据：10，10，10，9，9，8，3，9，8，10.

ⅲ．甲、乙、丙三种型号机器人除尘指数的平均数：

扫地机器人

甲

乙

丙

除尘指数平均数

8.6

8.6

m

根据以上信息，回答下列问题：

(1)、求表中m的值；

(2)、在抽取的扫地机器人中，如果除尘指数的10个数据的方差越小，则认为该型号的扫地机器人性能更稳定．据此推断：在甲、乙两种型号扫地机器人中，型扫地机器人的性能稳定（填“甲”或“乙”）；

(3)、在抽取的扫地机器人中，如果把10个除尘指数去掉一个最高值和一个最低值之后的平均值作为性能参考，平均值越高，则认为该型号扫地机器人性能表现越优秀．据此推断：在甲、乙、丙三种型号的扫地机器人中，表现最优秀的是（填“甲”、“乙”或“丙”）．

查看试题解析

选项	留空	多选	$A$	$B$	$C$	$D$
人数	$11$	$22$	$4209$	$3934$	$2057$	$1390$
占参考人数比 $(%)$	$0.09$	$0.19$	$36.21$	$33.85$	$17.7$	$11.96$

投稿篇数（篇）	1	2	3	4	5
七年级频数（人）	7	10	15	12	6
八年级频数（人）	2	10	13	21	4

统计量	中位数	众数	平均数	方差
七年级	3	3	$\bar{x}$	1.48
八年级	m	n	3.3	1.01

扫地机器人	甲	乙	丙
除尘指数平均数	8.6	8.6	m