2024年浙教版数学八年级下册阶段复习基础练第3章数据分析初步

试卷更新日期：2024-04-10 类型：复习试卷

进入出卷网下载

一、选择题

1. 某中学七（1）班的6位同学在课间体育活动时进行一分钟跳绳比赛，成绩（单位：个）如下：122，176，134，164，176，162，这组数据的众数和中位数分别是（）

A、162，164 B、176，140 C、176，149 D、176，163

查看试题解析
2. 某次乐器比赛共有11名选手参加且他们的得分都互不相同．现在知道这次比赛按选手得分由高到低顺序设置了6个获奖名额．若已知某位选手参加这次比赛的得分，要判断他能否获奖，则下列描述选手比赛成绩的统计量中，只需要知道（）

A、方差 B、平均数 C、众数 D、中位数

查看试题解析
3. 甲、乙两名射击运动员分别进行了相同次数的射击训练，如果将甲、乙两人射击环数的平均数分别记作 ${\bar{x}}_{甲}$ 和 ${\bar{x}}_{乙}$ ，方差分别记作 ${S^{2}}_{甲}$ 和 ${S^{2}}_{乙}$ ，那么下列描述能说明甲运动员成绩较好且更稳定的是（）

A、 ${\bar{x}}_{甲}$ ＞ ${\bar{x}}_{乙}$ 且 ${S^{2}}_{甲}$ ＜ ${S^{2}}_{乙}$ B、 ${\bar{x}}_{甲}$ ＞ ${\bar{x}}_{乙}$ 且 ${S^{2}}_{甲}$ 和＞ ${S^{2}}_{乙}$ C、 ${\bar{x}}_{甲}$ ＜ ${\bar{x}}_{乙}$ 且 ${S^{2}}_{甲}$ ＜ ${S^{2}}_{乙}$ D、 ${\bar{x}}_{甲}$ ＜ ${\bar{x}}_{乙}$ 且 ${S^{2}}_{甲}$ ＞ ${S^{2}}_{乙}$

查看试题解析
4. 样本数据2、 $a$ 、3、4的平均数是3，则 $a$ 的值是 $($ 　　 $)$

A、1 B、2 C、3 D、4

查看试题解析
5. 小明、小刚、小桐和小凯比赛谁投球比较远，每人投3次，结果如图所示．这四名同学中，（）投球的平均成绩大约是8米．

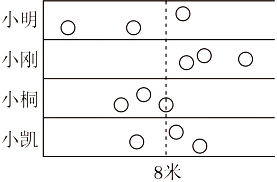A、小明 B、小刚 C、小桐 D、小凯

查看试题解析
6. 某商店销售 $5$ 种领口大小分别为 $38$ ， $39$ ， $40$ ， $41$ ， $42 ($ 单位： $c m)$ 的衬衫，一个月内的销量如下表：
领口大小 $/ c m$
     $38$
     $39$
     $40$
     $41$
     $42$
销量 $/$ 件
     $64$
     $199$
     $180$
     $110$
     $47$
你认为商店最感兴趣的是这里数据的（）

A、平均数 B、中位数 C、众数 D、加权平均数

查看试题解析
7. 某校举办了以“展礼仪风采，树文明形象”为主题的比赛．已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分，80分，80分，若依次按照 $30 ％， 45 ％， 25 ％$ 的百分比确定成绩，则该选手的成绩是（）

A、86分 B、85分 C、84分 D、83分

查看试题解析
8. 下列说法正确的是（　　）

A、一组数据2，2，3，4的众数是2，中位数是2.5 B、了解某市市民知晓“礼让行人”交通新规的情况，适合全面调查 C、甲、乙两人跳远成绩的方差分别为S²_甲＝3，S²_乙＝4，说明乙的跳远成绩比甲稳定 D、打开电视机，正在播放“襄阳新闻”是必然事件

查看试题解析

二、填空题

9. 若一组数据1，3，x，5，4，6的平均数是4，则这组数据的中位数是.

查看试题解析
10. 某校规定学生的体育成绩由三部分组成：体育课堂表现占成绩的 $20 %$ ，体育理论测试占 $30 %$ ，体育技能测试占 $50 %$ 。小颖的上述三项成绩依次是90分，80分，88分，则小颖这学期的体育成绩是分.

查看试题解析
11. 甲、乙两名同学的5次射击训练成绩(单位：环)如下表所示：
甲
7
8
9
8
8
乙
6
10
9
7
8
比较甲、乙这5次射击成绩的方差 $S_{甲}^{2} ， S_{乙}^{2}$ ，结果为 $S_{甲}^{2}$ $S_{乙}^{2}$ (填“>”“<”或“=”).

查看试题解析
12. 某公司要招聘一名职员，根据实际需要，从学历、经验和工作态度三个方面对甲、乙两名应聘者进行了测试．测试成绩如下表所示．如果将学历、经验和工作态度三项得分按2：1：3的比例确定两人的最终得分，并以此为依据确定录用者，那么将被录用（填甲或乙）

应聘者

项目

甲

乙

学历

9

8

经验

7

6

工作态度

5

7

查看试题解析

三、解答题

13. 某校八年级学生在一次射击训练中，随机抽取10名学生的成绩如下表，请回答问题：
环数
6
7
8
9
人数
1
5
3
$m$

(1)、填空：10名学生的射击成绩的众数是，中位数是， $m =$ ；

(2)、求这10名学生的平均成绩；

查看试题解析
14. 某校初三年级开展了系列交通安全知识竞赛，从中随机抽取30名学生两次知识竞赛的成绩(百分制)，并对数据(成绩)进行收集、整理、描述和分析.下面给出了部分信息.
a.这30名学生第一次竞赛成绩；
b.这30名学生两次知识竞赛的获奖情况统计表和第二次竞赛成绩得分情况统计图：（规定：分数≥90，获卓越奖；85≤分数＜90，获优秀奖；分数＜85，获参与奖）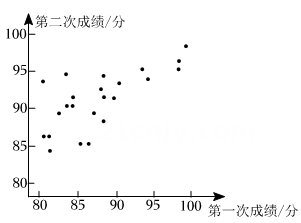

（规定：分数≥90，获卓越奖；85≤分数＜90，获优秀奖；分数＜85，获参与奖）
参与奖优秀奖卓越奖
第一次竞赛人数 10 10 10
平均分 82 87 95
第二次竞赛人数 2 12 16
平均分 84 87 93
c.第二次竞赛获卓越奖的学生成绩如下：90，90，91，91，91，91，92，93，93，94，94，94，95，95，96，98．
d.两次竞赛成绩样本数据的平均数、中位数、众数如表：
平均数中位数众数
第一次竞赛 m 87.5 88
第二次竞赛 90 n 91
根据以上信息，回答下列问题：

(1)、小松同学第一次竞赛成绩是89分，第二次竞赛成绩是91分，在图中用“O”圈出代表小松同学的点；

(2)、直接写出m，n的值；

(3)、请判断第几次竞赛中初三年级全体学生的成绩水平较高，并说明理由.

查看试题解析

15. 某学校为了解九年级学生体育训练情况，对九年级学生进行了一次体育模拟测试

.

测试
结束后，随机抽取了

(1)

班和

(2)

班各

20

名学生的测试成绩进行整理分析：

①

抽取的

(1)

班学生的测试成绩

(

单位：分

)

如下：

43

，

44

，

44

，

44

，

45

，

45

，

45

，

47

，

48

，

48

，

49

，

49

，

49

，

50

，

50

，

50

，

50

，

50

，

50

，

50 .

②

抽取的

(2)

班学生成绩

(

单位：分

)

用

x

表示，整理后分成如下五组：

A

组：

40 < x \leq 42

；

B

组：

42 < x \leq 44

：

C

组：

44 < x \leq 46

；

D

组：

46 < x \leq 48

；

E

组：

48 < x \leq 50 .

并绘制成如图所示扇形统计图，其中

D

组学生的成绩为：

47

，

47

，

48

，

48

，

48

，

48 .

抽取

(1)

班与

(2)

班学生测试成绩的平均数、中位数、众数如表所示：

班级	平均数	中位数	众数
$(1)$ 班	$47.5$	$48.5$	$c$
$(2)$ 班	$47.5$	$b$	$49$

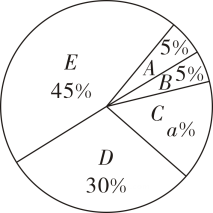(1)、根据上述信息可得：

a =

，

b =

，

c =

；

(2)、结合以上数据分析，你认为哪个班学生的体育成绩更好？请说明理由．

查看试题解析

领口大小 $/ c m$	$38$	$39$	$40$	$41$	$42$
销量 $/$ 件	$64$	$199$	$180$	$110$	$47$

		参与奖	优秀奖	卓越奖
第一次竞赛	人数	10	10	10
第一次竞赛	平均分	82	87	95
第二次竞赛	人数	2	12	16
第二次竞赛	平均分	84	87	93

甲	7	8	9	8	8
乙	6	10	9	7	8

应聘者项目	甲	乙
学历	9	8
经验	7	6
工作态度	5	7

环数	6	7	8	9
人数	1	5	3	$m$