2024年浙教版数学八年级下册阶段复习提高练第2章一元二次方程

试卷更新日期：2024-04-10 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知二次方程 $x^{2} + b x + c = 0$ 的两根为 $- 1$ 和5，则一次函数图象 $y = b x + c$ 不经过第（）象限

A、一 B、二 C、三 D、四

查看试题解析
2. 把一元二次方程 $(x + 3)^{2} = x (3 x - 1)$ 化成一般形式，正确的是（）

A、 $2 x^{2} - 7 x - 9 = 0$ B、 $2 x^{2} - 5 x - 9 = 0$ C、 $4 x^{2} + 7 x + 9 = 0$ D、 $2 x^{2} - 6 x - 10 = 0$

查看试题解析
3. 一元二次方程 $x^{2} + x - 1 = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
4. 用配方法解一元二次方程x²-8x+5=0，将其化成（x+a）²=b的形式，则变形正确的是（）

A、（x+4）²=11 B、（x-4）²=21 C、（x-8）²=11 D、（x-4）²=11

查看试题解析
5. 把一元二次方程 $3 x^{2} = 4 x - 1$ 化为一般式，当二次项为 $3 x^{2}$ 时，一次项和常数项分别为（）

A、 $4 x$ ， $- 1$ B、 $4 x$ ， 1 C、 $- 4 x$ ， $- 1$ D、 $- 4 x$ ， 1

查看试题解析
6. 扬帆中学有一块长 $30 m$ ，宽 $20 m$ 的矩形空地，计划在这块空地上划出四分之一的区域种花，小禹同学设计方案如图所示，求花带的宽度（花带等宽）．设花带的宽度为 $x$ $m$ ，则可列方程为 $($ 　　 $)$

A、 $(30 - x) (20 - x) = \frac{3}{4} \times 20 \times 30$ B、 $(30 - 2 x) (20 - x) = \frac{3}{4} \times 20 \times 30$ C、 $30 + 2 \times 20 x = \frac{1}{4} \times 20 \times 30$ D、 $(30 - 2 x) (20 - x) = \frac{1}{4} \times 20 \times 30$

查看试题解析
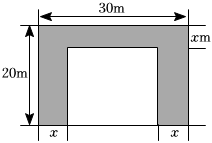7. 两千多年前，古希腊数学家欧多克索斯发现了黄金分割，黄金分割在日常生活中随处可见．例如：主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好．若舞台长10米，主持人从舞台一侧进人，设他至少走 $x$ 米时恰好站在舞台的黄金分割点上主持节目，则 $x$ 满足的方程是（）

A、 $(10 - x)^{2} = 10 x$ B、 $x^{2} = 10 (10 - x)$ C、 $x (10 - x) = 1 0^{2}$ D、 $x (10 - x) = 10 x^{2}$

查看试题解析
8. 下列说法正确的是 $($ 　　 $)$

A、对角线垂直的平行四边形是矩形 B、方程 $x^{2} + 4 x + 16 = 0$ 有两个相等的实数根 C、抛物线 $y = - x^{2} + 2 x + 3$ 的顶点为 $(1 ， 4)$ D、函数 $y = - \frac{2}{x}$ ， $y$ 随 $x$ 的增大而增大

查看试题解析

二、填空题

9. 若 $m$ 是方程 $2 x^{2} - x - 1 = 0$ 的一个根，则代数式 $4 m^{2} - 2 m$ 的值为．

查看试题解析
10. 若关于 $x$ 的方程 $x^{2} - 2 x + m = 0$ 有两个相等的实数根，则 $m =$ ．

查看试题解析
11. 某网络学习平台2021年的新注册用户数为100万，2023年的新注册用户数为64万，设新注册用户数的年平均下降率为 $x (0 < x < 1)$ ，则 $x =$ (用百分数表示).

查看试题解析
12. 定义新运算： $a ☆ b = a^{2} b + a b$ ．若关于x的方程 $x ☆ 2 = k$ 有两个实数根，则实数k的取值范围为．

查看试题解析

三、解答题

13. 若关于x的一元二次方程x²+bx-6=0有一个根是x=2，求b的值及方程的另一个根.

查看试题解析
14. 已知关于 $x$ 的二次三项式 $x^{2} + 18 x - m$ ．

(1)、若 $x^{2} + 18 x - m = 0$ 有两个相等的实数根，求 $m$ 的值；

(2)、嘉琪将其变形为 ${(x + 9)}^{2} + n$ 的形式，用含 $m$ 的式子表示 $n$ ．

查看试题解析
15. 第19届亚洲运动会于2023年9月23日晚在浙江省杭州市隆重开幕．亚运会吉祥物是一组承载深厚底蕴和充满时代活力的机器人，由“踪琮”、“莲莲”、“宸宸”共同组成“江南忆”组合，三个吉祥物造型形象生动，深受大家的喜爱．某网店购进一批亚运会吉祥物“宸宸”和“琮琮”，进货价和销售价如下表：
吉祥物
价格
宸宸
琮琮
进货价（元/个）
59
66
销售价（元/个）
79
88

(1)、该网店第一次用3160元购进“宸宸”和“踪琮”共50个，求购进“宸宸”和“琮琮”各多少个；

(2)、第一次购进的“宸宸”和“琮琮”售完后，该网店再次购进“宸宸”和“琮琮”共80个（进货价和销售价都不变），且进货总价不高于4900元，若进货后能全部售出，则应如何设计进货方案，才能获得最大销售利润，最大销售利润是多少：

(3)、亚运会临近结束时，该网店打算把“宸宸”调价销售，如果按照原价销售，平均每天可售8个，经调查发现，每降价1元，平均每天可多售2个，将销售价定为每个多少元时，才能使“宸宸”平均每天销售利润为288元．

查看试题解析