2024年浙教版数学八年级下册6.3反比例函数的应用课后培优练

试卷更新日期：2024-04-10 类型：同步测试

进入出卷网下载

一、选择题

1. 某杠杆装置如图，杆的一端吊起一桶水，阻力臂保持不变在使杠杆平衡的情况下，小康通过改变动力臂L，测量出相应的动力F数据如表.请根据表中数据规律探求，当动力臂L长度为2.0m时，所需动力最接近（）
动力臂L（m）
动力F（N）
0.5
600
1.0
302
1.5
200
2.0
a
2.5
120

A、120N B、151N C、300N D、302N

查看试题解析
2. 某品牌的饮水机接通电源就进入自动程序：开机加热到水温100℃，停止加热，水温开始下降，此时水温y(℃)与开机后用时.x(min)成反比例关系，直至水温降至30℃，饮水机关机.饮水机关机后即刻自动开机，重复上述自动程序.若在水温为30℃时，接通电源后，水温y(℃)和时间x(min)的关系如图所示，水温从100℃降到35℃所用的时间是（）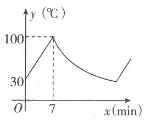

A、27min B、20min C、13min D、7min

查看试题解析
3. 为了预防流感，某中学用药熏消毒法对教室进行消毒.已知药物释放过程中，室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例，药物释放完毕后，y与x成反比例，整个过程中y关于x的函数图象如图所示.据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，则从药物释放完毕到学生能够进入教室，至少要经过（）

A、4.2小时 B、B.4小时 C、3.8小时 D、D.3.5小时

查看试题解析
4. 为预防春季流感，学校对教室进行喷雾消毒，喷雾阶段教室内每立方米空气中含药量y(mg)与时间x(min)成正比例，喷雾完成后y与x成反比例，其函数关系图象如图所示，已知当每立方米空气中含药量低于 1.6m g时，对人体方能无毒害作用，则下列说法正确的是（）

A、每立方米空气中含药量从6mg上升到8mg需要2min B、每立方米空气中含药量下降的过程中，y关于x 的函数表达式为 $y = \frac{20}{x}$ C、为了确保对人体无毒害作用，喷雾完成25 min 后学生才能进入教室 D、每立方米空气中含药量不低于4m g的持续时间为7.5min

查看试题解析
5. 某校科技小组进行野外考察，利用铺垫木板的方式，通过了一片湿泥地，他们发现：当人和木板对湿泥地的压力一定时，人和木板对地面的压强 p(Pa)随着木板面积S(m²)的变化而变化，其关系式为 p $= \frac{F}{S} (F \neq 0) .$ 如果人和木板对湿泥地的压力 F 合计600 N，那么下列说法正确的是（）

A、p是S的正比例函数 B、当S越来越大时，p也越来越大 C、若压强不超过6000 Pa，则木板面积最大为 0.1m² D、当木板面积为0.2m² 时，压强是3000 Pa

查看试题解析
6. 若电磁波波长λ(m)、频率 f(Hz)满足关系式 $λ f = 3 \times 10^{8} ，$ 则下列关于电磁波的说法中，正确的是（）

A、波长是频率的正比例函数 B、如果波长为 20 000 m，那么频率为1 500 Hz C、如果波长小于 30 000 m，那么频率小于10 000 Hz D、如果波长大于 50 000 m，那么频率小于6 000 Hz

查看试题解析
7. 如图，曲线表示温度T（℃）与时间t（h）之间的函数关系，它是一个反比例函数的图象的一支.当温度T≤2℃时，时间t应（）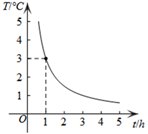

A、不小于 $\frac{2}{3}$ h B、不大于 $\frac{2}{3}$ h C、不小于 $\frac{3}{2}$ h D、不大于 $\frac{3}{2}$ h

查看试题解析
8. 在四个密闭容器中分别装有甲、乙、丙、丁四种气体，如图，用四个点分别描述这四种气体的密度 $ρ (k g / m^{2})$ 与体积 $V (m^{2})$ 的情况，其中描述乙、丁两种气体情况的点恰好在同一个反比例函数的阁象上，则这四种气体的质量最小的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

9. 某气球内充满一定质量的气体，当温度不变时，气球内气体的气压 $p (kPa)$ 是气体体积 $V (m^{3})$ 的反比例函数，其图象如图所示，当气球内的气压大于 $160 kPa$ 时，气球将爆炸，为了安全起见，气体的体积 $V$ 的取值范围．

查看试题解析
10. 如图，一块砖的A，B，C三个面的面积比是4：2：1，如果 B面向下放在地上时，地面所受压强为a(Pa)，那么 A面向下放在地上时，地面所受压强为Pa.

查看试题解析
11. 当温度不变时，气球内气体的压强 p(kPa)是气体体积V(m³)的函数，下表记录了一组实验数据：
V(m³)
1
1.5
2
2.5
3
p(kPa)
96
64
48
38.4
32
p关于V的函数表达式可能是。

查看试题解析
12. 油箱注满 $k$ 升油后，轿车可行驶的总路程 $S$ (单位：千米)与平均耗油量 $a$ (单位：升/千米)之间是反比例函数关系 $S = \frac{k}{a}$ ( $k$ 是常数， $k \neq 0)$ .已知某轿车油箱注满油后，以平均耗油量为每千米0.1升的速度行驶，可行驶700千米.则该轿车可行驶的总路程 $S$ 与平均耗油量 $a$ 之间的函数关系式为.

查看试题解析

三、解答题

13. 通过实验研究发现：初中生在数学课上听课注意力指标随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散学生注意力指标y随时间x(分钟)变化的函数图象如图所示，当0≤x<10和10≤x<20时，图象是线段；当20≤x≤45时，图象是反比例函数图象的一部分．

(1)、求点A对应的指标值

(2)、王老师在一节数学课上讲解一道数学综合题需要17分钟，他能否经过适当的安排，使学生在听这道综合题讲解时，注意力指标都不低于36？请说明理由．

查看试题解析
14. 某种商品上市之初采用了大量的广告宣传，其销售量与上市的天数之间成正比，当广告停止后，销售量与上市的天数之间成反比（如图），现已知上市30天时，当日销售量为120万件．

(1)、写出该商品上市以后销售量y（万件）与时间x（天数）之间的表达式；

(2)、求上市至第100天（含第100天），日销售量在36万件以下（不含36万件）的天数；

(3)、广告合同约定，当销售量不低于100万件，并且持续天数不少于12天时，广告设计师就可以拿到“特殊贡献奖”，那么本次广告策划，设计师能否拿到“特殊贡献奖”？

查看试题解析
15. 【项目式学习】
项目主题：守护生命，“数”说安全．
项目背景：随着社会的发展，安全问题变得日益重要．某校为了提高学生的安全意识，开展以“守护生命，'数'说安全”为主题的项目式学习活动．创新小组通过考察测量、模拟探究和成果迁移等环节，开展地下弯道对通行车辆长度的限制研究．

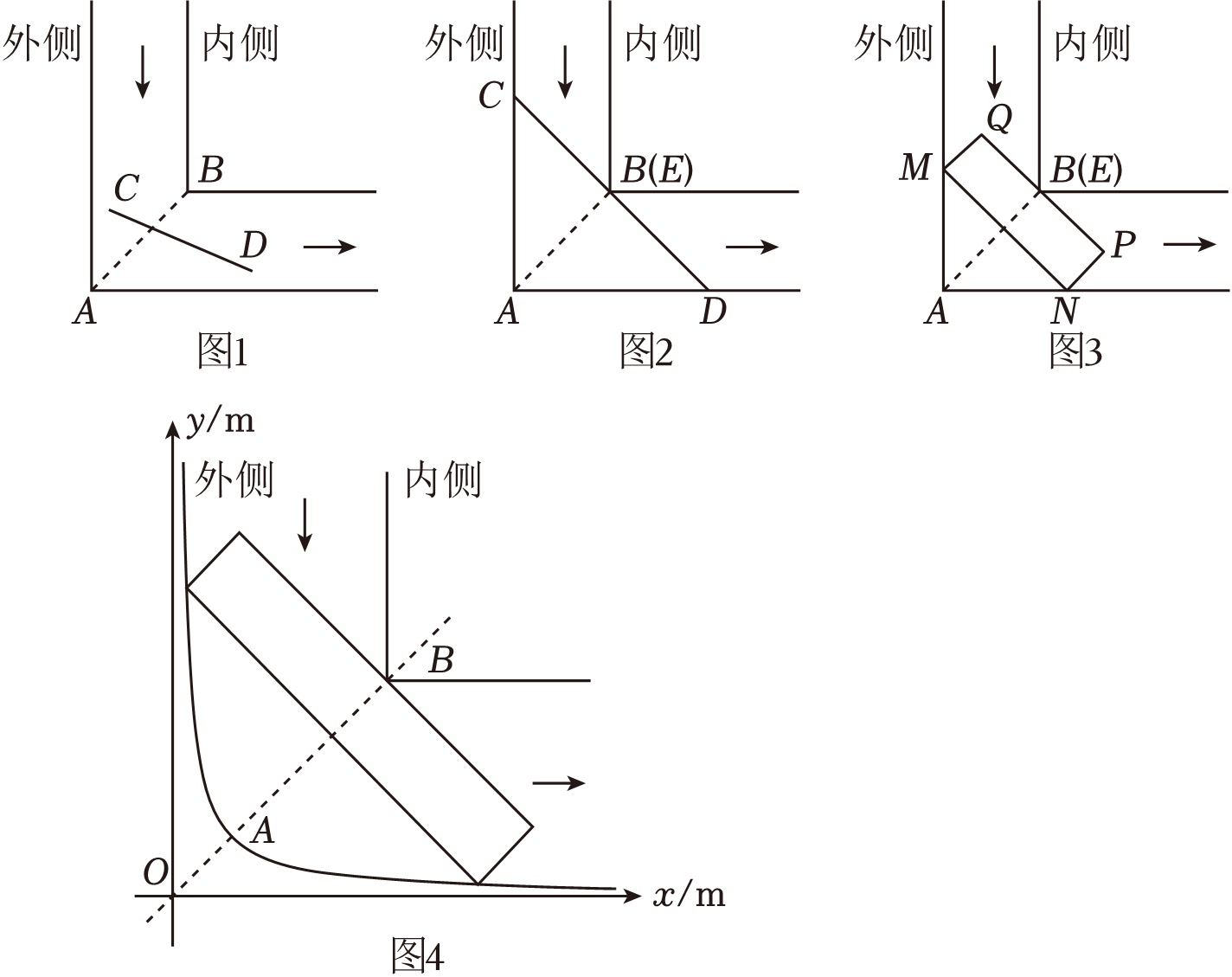
(1)、任务一：考察测量
如图1，创新小组所选取弯道的内、外侧均为直角，道路宽均为4m，则AB＝m；

(2)、任务二：模拟探究
如果汽车在行驶中与弯道内、外侧均无接触，则可安全通过．
创新小组用线段模拟汽车通过宽度相同的直角弯道，探究发现：
①当CD＜2AB时（如图1），线段CD能通过直角弯道；
②当CD＝2AB时，必然存在线段CD的中点E与点B重合的情况，线段CD恰好不能通过直角弯道（如图2）．此时，∠ADC的度数是；③当CD＞2AB时，线段CD不能通过直角弯道．

(3)、如图3，创新小组用矩形PQMN模拟汽车通过宽均为4m的直角弯道，发现当PQ的中点E与点B重合，且PQ⊥AB时，矩形PQMN恰好不能通过该弯道．若PQ＝am，PN＝2m，且矩形PQMN能通过该直角弯道，求a的最大整数值．

(4)、任务三：成果迁移
如图4，某弯道外侧形状可近似看成反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象，其对称轴交图象于点A．弯道内侧的顶点B在射线OA上，两边分别与x轴，y轴平行，OA＝2m，AB＝4 $\sqrt{2}$ m．创新小组探究发现通过该弯道的原理与通过直角弯道类似．有一辆长为bm，宽为2m的汽车需要安全通过该弯道，则b的最大整数值为．（参考数据： $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7， $\sqrt{5}$ ≈2.2， $\sqrt{7}$ ≈2.6）

查看试题解析

动力臂L（m）	动力F（N）
0.5	600
1.0	302
1.5	200
2.0	a
2.5	120

V(m³)	1	1.5	2	2.5	3
p(kPa)	96	64	48	38.4	32