2024年浙教版数学八年级下册6.2反比例函数的图像和性质课后培优练
试卷更新日期:2024-04-10 类型:同步测试
一、选择题
-
1. 下列关于反比例函数的说法,错误的是( )A、它的图象位于第一、三象限 B、点(1,6)在它的图象上 C、它的图象关于原点成中心对称 D、当x₁>x₂时,y₁<y₂2. 若图中反比例函数的表达式均为 则阴影部分面积为 2的是 ( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,在平面直角坐标系中,M为x轴正半轴上一点,过点 M 的直线l∥y轴,且分别与反比例函数和 (x>0,k≠0)的图象相交于 P,Q两点.若 , 则 k 的值为( )
3. 如图,在平面直角坐标系中,M为x轴正半轴上一点,过点 M 的直线l∥y轴,且分别与反比例函数和 (x>0,k≠0)的图象相交于 P,Q两点.若 , 则 k 的值为( ) A、38 B、22 C、-7 D、-224. 如图,在反比例函数 的图象上有点 P₁,P₂,P₃,它们的横坐标依次为1,3,6,分别过这些点作x轴与y轴的垂线段.若图中阴影部分的面积分别记为 S₁,S₂,且S₂=3,则 S₁的值为( )
A、38 B、22 C、-7 D、-224. 如图,在反比例函数 的图象上有点 P₁,P₂,P₃,它们的横坐标依次为1,3,6,分别过这些点作x轴与y轴的垂线段.若图中阴影部分的面积分别记为 S₁,S₂,且S₂=3,则 S₁的值为( ) A、3 B、4 C、5 D、65. 如图是同一平面直角坐标系中函数 y1=2x和 的图象.观察图象可得不等式 的解为( )
A、3 B、4 C、5 D、65. 如图是同一平面直角坐标系中函数 y1=2x和 的图象.观察图象可得不等式 的解为( ) A、-1<x<1 B、x<-1或x>1 C、x<-1或0<x<1 D、-1<x<0 或x>16. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( )
A、-1<x<1 B、x<-1或x>1 C、x<-1或0<x<1 D、-1<x<0 或x>16. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、47. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( )
A、1 B、 C、2 D、47. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( ) A、 B、 C、 D、8. 如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1 , A2 , …An , 连结A1P2 , A2P3 , …An-1Pn , 再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )
A、 B、 C、 D、8. 如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1 , A2 , …An , 连结A1P2 , A2P3 , …An-1Pn , 再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )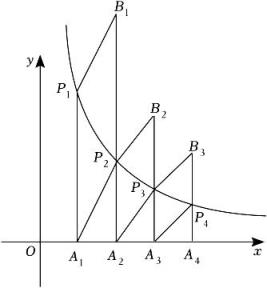 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在平面直角坐标系xOy中,直线y=kx(k <0)与反比例函数的图象相交于A,C两点,D为x轴负半轴上一点,连结CD 并延长,交反比例函数 的图象于点B.若CB =2CD,△CDO的面积为1,则m-n=.
 10. 如图,菱形的边在x轴的正半轴上,反比例函数的图象经过菱形对角线的中点D和顶点C,若菱形的面积为 , 则点C的坐标为 .
10. 如图,菱形的边在x轴的正半轴上,反比例函数的图象经过菱形对角线的中点D和顶点C,若菱形的面积为 , 则点C的坐标为 .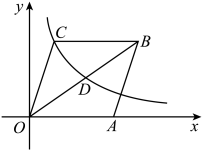 11. 如图,已知点、、 . 直线轴,垂足为点 . 其中 , 若△与关于直线对称,且△有两个顶点在函数的图象上,则的值为 .
11. 如图,已知点、、 . 直线轴,垂足为点 . 其中 , 若△与关于直线对称,且△有两个顶点在函数的图象上,则的值为 .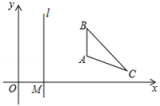
三、解答题
-
12. 设函数 函数 (k1、k2、b是常熟,k1≠0,k2≠0).(1)、若函数y1和函数 y₂的图象相交于点 A (1,m),B(3,1),
①求函数 y₁,y₂ 的表达式.
②当2<x<3时,比较 y₁ 与y₂的大小(直接写出结果).
(2)、若点 C(2,n)在函数 y₁ 的图像上,点 C 先向下平移 2个单位,再向左平移4 个单位,得点D.若点 D 恰好落在函数 y₁ 的图像上,求 n 的值.13. 如图,矩形ABCO在平面直角坐标系中,点A(-5,0),C(0,6),反比例函数图象 L₁ 对应的函数表达式为 反比例函数图象 L₂ 对应的函数表达式为 把矩形 ABCO内部(不含边界)横、纵坐标均为整数的点称为“整点”.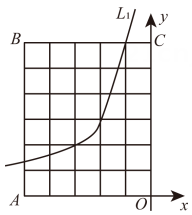 (1)、若 k=-12,则L₂和L₁ 之间(不含边界)有个“整点”.(2)、若L₂ 和L₁之间(不含边界)有4个“整点”,求k的取值范围.14. 如图,一次函数y1=kx+b(k≠0)与函数为y2=(x>0)的图象交于A(4,1),B( , a )两点
(1)、若 k=-12,则L₂和L₁ 之间(不含边界)有个“整点”.(2)、若L₂ 和L₁之间(不含边界)有4个“整点”,求k的取值范围.14. 如图,一次函数y1=kx+b(k≠0)与函数为y2=(x>0)的图象交于A(4,1),B( , a )两点 (1)、求这两个函数的表达式;(2)、根据图象,直接写出满足y1-y2>0时x的取值范围;(3)、点P在线段AB上,过点P作x轴的垂线,垂足为M,交函数y2的图象于点Q,若△POQ面积为3,求点P的坐标.15. 如图,一次函数y=mx+1的图象与反比例函数y=的图象相交于A、B两点,点C在x轴正半轴上,点D(1,-2),连接OA、OD、DC、AC , 四边形OACD为菱形.
(1)、求这两个函数的表达式;(2)、根据图象,直接写出满足y1-y2>0时x的取值范围;(3)、点P在线段AB上,过点P作x轴的垂线,垂足为M,交函数y2的图象于点Q,若△POQ面积为3,求点P的坐标.15. 如图,一次函数y=mx+1的图象与反比例函数y=的图象相交于A、B两点,点C在x轴正半轴上,点D(1,-2),连接OA、OD、DC、AC , 四边形OACD为菱形. (1)、求一次函数与反比例函数的解析式;(2)、根据图象,直接写出反比例函数的值小于2时,x的取值范围;(3)、设点P是直线AB上一动点,且S△OAP=S菱形OACD , 求点P的坐标.
(1)、求一次函数与反比例函数的解析式;(2)、根据图象,直接写出反比例函数的值小于2时,x的取值范围;(3)、设点P是直线AB上一动点,且S△OAP=S菱形OACD , 求点P的坐标.