2024年浙教版数学八年级下册5.3正方形课后培优练
试卷更新日期:2024-04-10 类型:同步测试
一、选择题
-
1. 下列命题中,假命题是( )A、平行四边形的对角线相等 B、正方形的对角线互相垂直平分 C、对角线互相垂直的平行四边形是菱形 D、有一个角为的平行四边形是矩形2. 在周长为 的正方形 中,点 是 边的中点,点 为对角线 上的一个动点,则 的最小值为( )
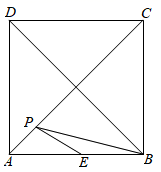 A、2 B、 C、 D、3. 如图,点M是正方形ABCD内位于对角线BD下方的一点, ,则 为( )
A、2 B、 C、 D、3. 如图,点M是正方形ABCD内位于对角线BD下方的一点, ,则 为( )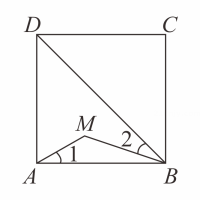 A、120° B、130° C、125° D、135°4. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( )
A、120° B、130° C、125° D、135°4. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( )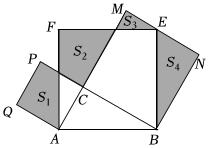 A、 B、 C、 D、5. 如图,分别沿长方形纸片和正方形纸片 EFGH 的对角线 , 剪开,拼成如图2所示的四边形 , 若中间空白部分四边形恰好是正方形 , 且四边形的面积为50,则正方形的面积是( )
A、 B、 C、 D、5. 如图,分别沿长方形纸片和正方形纸片 EFGH 的对角线 , 剪开,拼成如图2所示的四边形 , 若中间空白部分四边形恰好是正方形 , 且四边形的面积为50,则正方形的面积是( ) A、 B、 C、 D、6. 如图,在正方形中,点、分别是边、上的两个动点不与顶点、、重合 , 在运动中始终保持 , 与交于点 , 当时,的度数为( )
A、 B、 C、 D、6. 如图,在正方形中,点、分别是边、上的两个动点不与顶点、、重合 , 在运动中始终保持 , 与交于点 , 当时,的度数为( )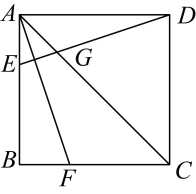 A、 B、 C、 D、7. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )
A、 B、 C、 D、7. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )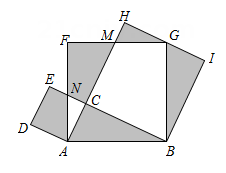 A、 B、 C、 D、8. 如图,在正方形ABCD中,点E在边CD上,点H在边AD上,CE=DH , CH交BE于点F , 交BD于点G , 连接GE . 下列结论:①CH=BE;②CH⊥BE;③S△GCE=S△GDH;④当E是CD的中点时,;⑤当EC=2DE时,S正方形ABCD=6S四边形DEGH . 其中正确结论的序号是( )
A、 B、 C、 D、8. 如图,在正方形ABCD中,点E在边CD上,点H在边AD上,CE=DH , CH交BE于点F , 交BD于点G , 连接GE . 下列结论:①CH=BE;②CH⊥BE;③S△GCE=S△GDH;④当E是CD的中点时,;⑤当EC=2DE时,S正方形ABCD=6S四边形DEGH . 其中正确结论的序号是( ) A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤
A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤二、填空题
-
9. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.将小正方形对角线双向延长,分别交边 , 和边的延长线于点G,H.若大正方形与小正方形的面积之比为5, , 则大正方形的边长为 .
 10. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .
10. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .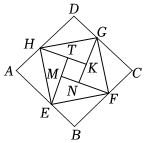 11. 如图,正方形的边长为8,点为边上一点,且 , 点为边上的一个动点,连接 , 以为一条直角边向右侧作等腰 , 且使 , 连接 , 则的最小值是 .
11. 如图,正方形的边长为8,点为边上一点,且 , 点为边上的一个动点,连接 , 以为一条直角边向右侧作等腰 , 且使 , 连接 , 则的最小值是 .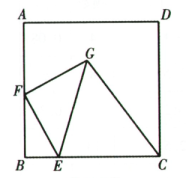 12. 如图正方形的边长为3,E是上一点且 , F是线段上的动点.连接 , 将线段绕点C逆时针旋转 90°得到 , 连接 , 则的最小值是 .
12. 如图正方形的边长为3,E是上一点且 , F是线段上的动点.连接 , 将线段绕点C逆时针旋转 90°得到 , 连接 , 则的最小值是 .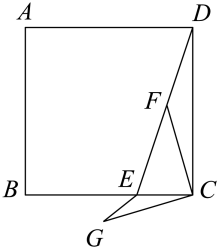
三、解答题
-
13. 如图,已知在正方形中, , 点为线段上一点点不与、重合 , 连接 , 过点作交射线于点 , 以、为邻边作矩形 .
 (1)、求证:;(2)、连接 , 设 , 的面积为求关于的函数关系式并写出自变量的取值范围;(3)、当时,求的度数.14. 如图1,两张纸片正方形与正方形拼在一起,在边上取 , 沿 , 分别剪一刀,将拼至 , 拼至 , 无缝隙无重叠,如图2.
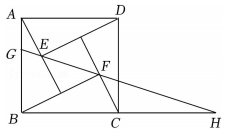
(1)、求证:;(2)、连接 , 设 , 的面积为求关于的函数关系式并写出自变量的取值范围;(3)、当时,求的度数.14. 如图1,两张纸片正方形与正方形拼在一起,在边上取 , 沿 , 分别剪一刀,将拼至 , 拼至 , 无缝隙无重叠,如图2.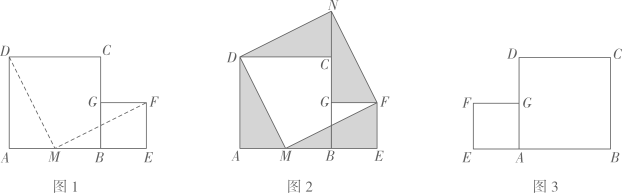 (1)、求证: .(2)、求证:四边形是正方形.(3)、仿照题中的剪拼方法,剪两刀把图3中两个正方形剪拼成一个更大的正方形,在图中作出剪拼线,并完成拼图.15. 如图1,矩形ABCD中,过对角线AC的中点O画EF⊥AC分别交AB,CD于点E,F,连结AF,CE.
(1)、求证: .(2)、求证:四边形是正方形.(3)、仿照题中的剪拼方法,剪两刀把图3中两个正方形剪拼成一个更大的正方形,在图中作出剪拼线,并完成拼图.15. 如图1,矩形ABCD中,过对角线AC的中点O画EF⊥AC分别交AB,CD于点E,F,连结AF,CE.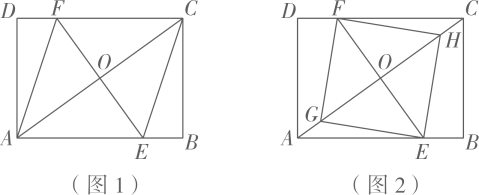 (1)、[证明体验]
(1)、[证明体验]求证:四边形AECF是菱形.
(2)、[基础巩固]若AB=8,BC=6,求菱形AECF的边长.
(3)、[拓展延伸]如图2,在对角线AC上取点G,H,使得四边形EHFG是正方形,若正方形EHFG的边长为 , 且AE=5CH,求矩形ABCD的面积.