2024年浙教版数学八年级下册5.3正方形课后提高练
试卷更新日期:2024-04-10 类型:同步测试
一、填空题
-
1. 如图,四边形ABCD是正方形,延长AB至点E,使AE=AC,连结CE,则∠BCE的度数为°.
 2. 如图,三个边长均为2的正方形重叠在一起,O₁,O₂是其中两个正方形的中心,则阴影部分的面积是.
2. 如图,三个边长均为2的正方形重叠在一起,O₁,O₂是其中两个正方形的中心,则阴影部分的面积是. 3. 如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连结AF,DE.若∠FAC=15°,则∠AED的度数为
3. 如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连结AF,DE.若∠FAC=15°,则∠AED的度数为 4. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .
4. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .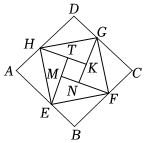
二、解答题
-
5. 如图,是的一条角平分线,交于点E , 交于点F .
 (1)、求证:四边形是菱形;(2)、若 , 当 ▲ 度时,四边形为正方形并证明.6. 如图,正方形 ABCD 的边长为4,E 为BC 边上的一点,BE=1,F为AB 的中点.若 P 为对角线AC 上的一个动点,求 PF+PE的最小值.
(1)、求证:四边形是菱形;(2)、若 , 当 ▲ 度时,四边形为正方形并证明.6. 如图,正方形 ABCD 的边长为4,E 为BC 边上的一点,BE=1,F为AB 的中点.若 P 为对角线AC 上的一个动点,求 PF+PE的最小值.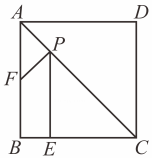 7. 如图,在△ABC中,AB=AC,AD是BC 边上的中线,E 是 AD 上一点,过点 B作BF∥EC,交AD的延长线于点F,连结BE,CF.
7. 如图,在△ABC中,AB=AC,AD是BC 边上的中线,E 是 AD 上一点,过点 B作BF∥EC,交AD的延长线于点F,连结BE,CF.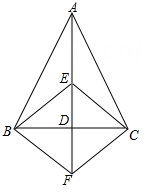 (1)、求证:△BDF≌△CDE.(2)、当 ED 与BC 满足什么数量关系时,四边形BECF 是正方形? 请说明理由.
(1)、求证:△BDF≌△CDE.(2)、当 ED 与BC 满足什么数量关系时,四边形BECF 是正方形? 请说明理由.三、选择题
-
8. 如图,四边形是平行四边形,下列结论中错误的是( )
 A、当时,是矩形 B、当时,是菱形 C、当是正方形时, D、当是菱形时,9. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
A、当时,是矩形 B、当时,是菱形 C、当是正方形时, D、当是菱形时,9. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( ) A、1 B、 C、 D、10. 有下列四个命题:①一组对边平行且一组对角相等的四边形是平行四边形;②对角线互相垂直且相等的四边形是正方形;③矩形的对角线平分一组对角;④正五边形既是轴对称图形又是中心对称图形.其中真命题是( )A、②③④ B、②④ C、①② D、①11. 如图,在正方形ABCD中,E,F 分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是 ( )
A、1 B、 C、 D、10. 有下列四个命题:①一组对边平行且一组对角相等的四边形是平行四边形;②对角线互相垂直且相等的四边形是正方形;③矩形的对角线平分一组对角;④正五边形既是轴对称图形又是中心对称图形.其中真命题是( )A、②③④ B、②④ C、①② D、①11. 如图,在正方形ABCD中,E,F 分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是 ( )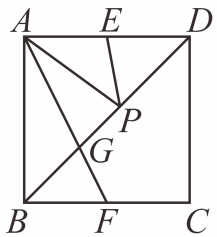 A、AB B、DG C、BD D、AF12. 如图,在平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC 是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为 ( )
A、AB B、DG C、BD D、AF12. 如图,在平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC 是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为 ( ) A、-2 B、 C、 D、13. 如图,在边长为4的正方形ABCD中,∠CDE=30°,DE⊥CF,则AF 的长为 ( )
A、-2 B、 C、 D、13. 如图,在边长为4的正方形ABCD中,∠CDE=30°,DE⊥CF,则AF 的长为 ( )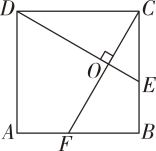 A、 B、 C、 D、
A、 B、 C、 D、