2024年浙教版数学八年级下册5.2菱形课后培优练
试卷更新日期:2024-04-10 类型:同步测试
一、选择题
-
1. 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
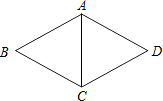 A、5 B、10 C、15 D、202. 菱形具有而矩形不一定具有的性质是 ( )
A、5 B、10 C、15 D、202. 菱形具有而矩形不一定具有的性质是 ( )
A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补3. 如图,数学实践活动课上小明用两根木条钉成一个角形框架 , 且 , , 将一根橡皮筋两端固定在点A,B处,拉展成线段AB,在平面内,拉动橡皮筋上的一点 , 当四边形OACB是菱形时,橡皮筋再次被拉长了( )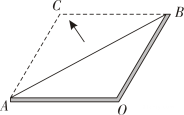 A、 B、 C、 D、4. 如图,菱形的对角线 , 相交于点 , 过点作于点 , 连接若 , 菱形的面积为 , 则的长为( )
A、 B、 C、 D、4. 如图,菱形的对角线 , 相交于点 , 过点作于点 , 连接若 , 菱形的面积为 , 则的长为( ) A、 B、 C、 D、5. 如图,四边形是菱形, , , 于点 , 则的长为( )
A、 B、 C、 D、5. 如图,四边形是菱形, , , 于点 , 则的长为( ) A、 B、 C、 D、6. 如图,菱形的对角线、相交于点 , 过点作于点 , 连接 , 若 , , 则的长为( )
A、 B、 C、 D、6. 如图,菱形的对角线、相交于点 , 过点作于点 , 连接 , 若 , , 则的长为( ) A、 B、 C、 D、7. 如图,四边形是菱形,过点的直线分别交 , 的延长线于点 , , 若 , , 则等于( )
A、 B、 C、 D、7. 如图,四边形是菱形,过点的直线分别交 , 的延长线于点 , , 若 , , 则等于( )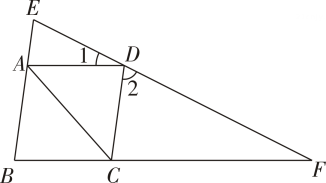 A、 B、 C、 D、8. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
A、 B、 C、 D、8. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
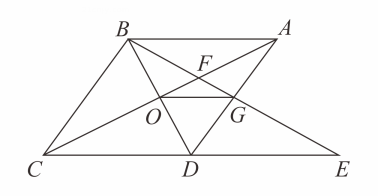
;与全等的三角形共有个;
;由点、、、构成的四边形是菱形.
A、 B、 C、 D、二、填空题
-
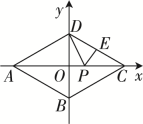
9. 菱形ABCD,点A,B,C,D均在坐标轴上. ∠ABC=120°,点A(-6,0),点E是CD的中点,点P是OC上的一动点,则△PDE周长的最小值是 .
 10. 如图,菱形的对角线长度为6,边长 , M为菱形外一个动点,满足 , N为中点,连接 . 则当M运动的过程中,长度的最大值为.
10. 如图,菱形的对角线长度为6,边长 , M为菱形外一个动点,满足 , N为中点,连接 . 则当M运动的过程中,长度的最大值为.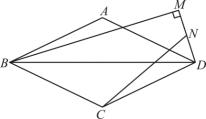 11. 如图,在菱形ABCD中, , , 点E为对角线BD上一动点(不与点B重合),且 , 连接CE交DA延长线于点F.
11. 如图,在菱形ABCD中, , , 点E为对角线BD上一动点(不与点B重合),且 , 连接CE交DA延长线于点F.①;
②当△AEF为直角三角形时,;
③当△AEF为等腰三角形时,或者;
④连接BF,当时,FC平分∠AFB.
以上结论正确的是.(填正确的序号).
 12. 如图,直线与轴、轴分别交于、两点,是的中点,是上一点,四边形是菱形,其中点坐标为 , , 则的面积为 .
12. 如图,直线与轴、轴分别交于、两点,是的中点,是上一点,四边形是菱形,其中点坐标为 , , 则的面积为 .
三、解答题
-
13. 如图,在▱ABCD中,AB=6 cm,BC=10 cm,∠B=60°,G是CD的中点,E是边AD 上的动点,EG 的延长线与BC 的延长线相交于点 F,连结 CE,DF.
 (1)、求证:四边形CEDF 是平行四边形.(2)、①当AE= cm时,四边形CEDF 是菱形,请说明理由.
(1)、求证:四边形CEDF 是平行四边形.(2)、①当AE= cm时,四边形CEDF 是菱形,请说明理由.②当 AE= cm时,四边形 CEDF 是矩形,请说明理由.
14. 如图,直线y=x-3与x轴交于点C,与y轴交于点D,直线y=kx+b与y轴交于点B(0,4),与直线y=x-3交于点A(m,1). (1)、求直线AB的表达式;(2)、点P是直线CD上的一个动点,连接PB,当△PBA的面积为7时,求点P的坐标;(3)、E为y轴上的点,F在坐标平面内,以点A,B,E,F为顶点的四边形是菱形,请直接写出符合条件的点F的坐标.15. 已知:如图,直线与x轴相交于点A,与直线交于点P.
(1)、求直线AB的表达式;(2)、点P是直线CD上的一个动点,连接PB,当△PBA的面积为7时,求点P的坐标;(3)、E为y轴上的点,F在坐标平面内,以点A,B,E,F为顶点的四边形是菱形,请直接写出符合条件的点F的坐标.15. 已知:如图,直线与x轴相交于点A,与直线交于点P. (1)、求点P的坐标.(2)、动点F从原点O出发,以每秒1个单位的速度在线段OA上向点A作匀速运动,连接PF,设运动时间为t秒,△PFA的面积为S,求出S关于t的函数关系式.(3)、若点M是y轴上任意一点,点N是坐标平面内任意一点,若以O、M、N、P为顶点的四边形是菱形,请直接写出点N的坐标.
(1)、求点P的坐标.(2)、动点F从原点O出发,以每秒1个单位的速度在线段OA上向点A作匀速运动,连接PF,设运动时间为t秒,△PFA的面积为S,求出S关于t的函数关系式.(3)、若点M是y轴上任意一点,点N是坐标平面内任意一点,若以O、M、N、P为顶点的四边形是菱形,请直接写出点N的坐标.