2024年浙教版数学八年级下册4.2平行四边形课后提高练
试卷更新日期:2024-04-10 类型:同步测试
一、选择题
-
1. 两条平行线之间的距离是指( )A、两条平行线中,从一条直线上任意一点到另一条直线的垂线段 B、两条平行线中,从一条直线上任意一点到另一条直线的垂线段的长度 C、两条平行线中,从一条直线上任意一点到另一条直线的垂线的长度. D、两条平行线中,从一条直线上任意一点到另一条直线上的一点间线段的长度2. 如图,在▱ABCD 中,AC 与 BD 相交于点O,∠ODA=90°,OA=6,OB=2,则AD的长是( )
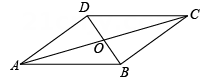 A、6 B、4 C、4 D、43. 如图,在平行四边形中,点是延长线上的一点,且 , 则的度数是( )
A、6 B、4 C、4 D、43. 如图,在平行四边形中,点是延长线上的一点,且 , 则的度数是( )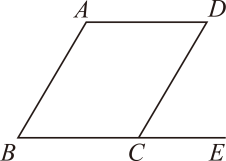 A、 B、 C、 D、4. 如图,平行四边形的对角线 , 交于点 , 已知 , , 的周长为15,则的长为( )
A、 B、 C、 D、4. 如图,平行四边形的对角线 , 交于点 , 已知 , , 的周长为15,则的长为( ) A、5 B、6 C、7 D、85. 如图,A,P是直线m 上的任意两点,B,C是直线n上的两个定点,且m∥n,则下列说法正确的是( )
A、5 B、6 C、7 D、85. 如图,A,P是直线m 上的任意两点,B,C是直线n上的两个定点,且m∥n,则下列说法正确的是( ) A、AC=BP B、△ABC的周长等于△BCP 的周长 C、△ABC的面积等于△ABP的面积 D、△ABC的面积等于△PBC的面积6. 如图,点A在平行四边形的对角线上,则图中两个阴影三角形的面积S₁,S₂的大小关系是( )
A、AC=BP B、△ABC的周长等于△BCP 的周长 C、△ABC的面积等于△ABP的面积 D、△ABC的面积等于△PBC的面积6. 如图,点A在平行四边形的对角线上,则图中两个阴影三角形的面积S₁,S₂的大小关系是( ) A、 B、 C、 D、无法确定7. 如图,在▱ABCD中,O是对角线AC上一点,连结 BO,DO.若△COD,△AOD,△AOB,△BOC 的面积分别为 S1 , S2 , S3 , S4 , 则下列关于 S1 , S2 , S3 , S4的等量关系中,不一定正确的是( )
A、 B、 C、 D、无法确定7. 如图,在▱ABCD中,O是对角线AC上一点,连结 BO,DO.若△COD,△AOD,△AOB,△BOC 的面积分别为 S1 , S2 , S3 , S4 , 则下列关于 S1 , S2 , S3 , S4的等量关系中,不一定正确的是( ) A、 B、 C、 D、8. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )
A、 B、 C、 D、8. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )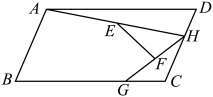 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
9. 在□ABCD中,若∠A+∠C=100°,则∠D的度数为°.10. 如图,在▱ABCD中,过点 B 作 BM⊥AC 于点E,交 CD于点 M,过点 D作 DN⊥AC 于点 F,交 AB于点 N,AF=12,EM=5.若 AD=15,则直线AB 与CD之间的距离为.
 11. 如图,在▱ABCD中,若AB=4,BC=6,AC的垂直平分线交AD于点E,连结CE,则△CDE的周长为.
11. 如图,在▱ABCD中,若AB=4,BC=6,AC的垂直平分线交AD于点E,连结CE,则△CDE的周长为. 12. 如图,在▱ABCD中,BF平分∠ABC,交 AD 于点F,CE平分∠BCD,交 AD于点E.若AB=8,EF=1,则BC长为.
12. 如图,在▱ABCD中,BF平分∠ABC,交 AD 于点F,CE平分∠BCD,交 AD于点E.若AB=8,EF=1,则BC长为.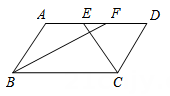
三、解答题
-
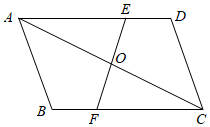
13. 如图,在 中,点 , 分别在 、 上,且 ,连接 , 交于点 .求证: .
 14. 如图,四边形 ABCD 是平行四边形,点A,B在x轴上,点 D在y轴上,AD=6,AB=8,点 A 的坐标为(-3,0).求点 B,C,D的坐标.
14. 如图,四边形 ABCD 是平行四边形,点A,B在x轴上,点 D在y轴上,AD=6,AB=8,点 A 的坐标为(-3,0).求点 B,C,D的坐标.
四、综合题
-
15. 如图①,在平行四边形ABCD中, AB=3,AD=6.动点P沿AD边以每秒个单位长度的速度从点A向终点D .设点P运动的时间为t(t>0)秒.
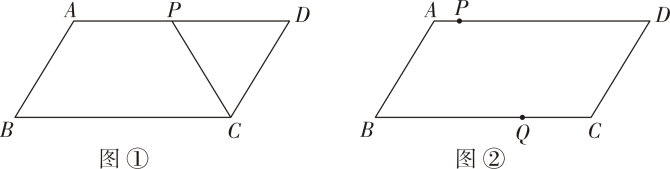 (1)、线段PD的长为 (用含t的代数式表示).(2)、当CP平分∠BCD时,求t的值.(3)、如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,点Q也随之停止运动.当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.
(1)、线段PD的长为 (用含t的代数式表示).(2)、当CP平分∠BCD时,求t的值.(3)、如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,点Q也随之停止运动.当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.