广东省湛江市廉江市良垌三中2023-2024学年七年级下学期数学第一次月考试卷

试卷更新日期：2024-04-10 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项符合题目要求。）

1. 下列语句是命题的是（）

A、画一条直线 B、正数都大于零 C、多彩的青春 D、明天晴天吗？

查看试题解析
2. 2023年9月23日至10月8日第19届亚运会在杭州举行，杭州会徽的标志如下图所示，以下通过平移这个标志得到的图形是（）

A、 B、 C、 D、

查看试题解析
3. 如图，设点 $P$ 是直线 $l$ 外一点， $P Q ⊥ l$ ，垂足为点 $Q$ ，点 $T$ 是直线 $l$ 上的一个动点，连接PT，则（）

A、 $P T \geq P Q$ B、 $P T \leq P Q$ C、 $P T > P Q$ D、 $P T < P Q$

查看试题解析
4. 如图，直线AB、CD相交于点 $O$ ，若 $O E ⊥ A B, ∠ D O E = 5 8^{°}$ ，则 $∠ A O C$ 等于（）

A、 $5 8^{°}$ B、 $4 2^{°}$ C、 $3 2^{°}$ D、 $2 2^{°}$

查看试题解析
5. 世界上最早记载潜望镜原理的古书，是公元前二世纪中国的《淮南万毕术》．书中记载了这样的一段话：“取大镜高悬，置水盘于其下，则见四邻矣”.现代潜艇潜望镜是在20世纪初发明的．如图是潜望镜工作原理的示意图，那么它所应用的数学原理是（）

A、内错角相等，两直线平行 B、同旁内角互补，两直线平行 C、对顶角相等 D、两点确定一条直线

查看试题解析
6. 如图，水面AB与水杯下沿CD平行，光线EF从水中射向空气时发生折射，光线变成FH，点 $G$ 在射线EF上，已知 $∠ H F B = 2 0^{°}, ∠ F E D = 4 5^{°}$ ，则 $∠ G F H$ 的度数是（）

A、 $2 5^{°}$ B、 $3 5^{°}$ C、 $4 5^{°}$ D、 $2 0^{°}$

查看试题解析
7. 如图，点 $E$ 在BC的延长线上，下列条件中，能判断 $A B / / C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ D = ∠ 5$ D、 $∠ D + ∠ B C D = 18 0^{°}$

查看试题解析
8. 如图，直线AB与CD相交于点E，EF平分 $∠ C E B, F M / / A B$ ．若 $∠ F = 7 0^{°}$ ，则 $∠ 3 = ()$

A、 $7 0^{°}$ B、 $4 0^{°}$ C、 $5 0^{°}$ D、 $3 0^{°}$

查看试题解析
9. 如图，点 $O A ⊥ O D$ ， $O B ⊥ O E$ ， $O C ⊥ O F$ ，且 $∠ A O B = 25 °$ ， $∠ E O F = 35 °$ ，则与 $∠ C O D$ 是（）

A、 $30 °$ B、 $35 °$ C、 $25 °$ D、 $40 °$

查看试题解析
10. 如图， $A B / / C D, E$ 为AB上一点，且 $E F ⊥ C D$ 垂足为 $F, ∠ C E D = 9 0^{°}, C E$ 平分 $∠ A E G$ ，且 $∠ C G E = α$ ，则下列结论：① $∠ A E C = 9 0^{°} - \frac{1}{2} α$ ；②DE平分 $∠ G E B$ ；③ $∠ C E F = ∠ G E D$ ；④ $∠ F E D + ∠ B E C = 18 0^{°}$ ；其中正确的有（）

A、①② B、②③④ C、①②③④ D、①③④

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 将命题“邻补角互补”改写成“如果……，那么……”的形式：.

查看试题解析
12. 如图， $A C ⊥ B C, A C = 9, B C = 12, A B = 15$ ．点 $A$ 到直线BC的距离是，点 $B$ 到直线AC的距离是.

查看试题解析
13. 如图是地球截面图，其中 $A B$ ， $C D$ 分别表示赤道和南回归线，冬至正午时，太阳光直射南回归线（太阳光线 $M D$ 的延长线经过地心 $O$ ），此时，太阳光线与地面水平线 $E F$ 垂直，已知 $∠ M D N = 23 ° 2 6^{'}$ ，则 $∠ E D N$ 的度数是．

查看试题解析
14. 如图，将边长为 $3 c m$ 的等边 $△ A B C$ 沿着边BC向右平移 $2 c m$ ，得到 $△ D E F$ ，则四边形ABFD的周长为.

查看试题解析
15. 如图，点 $E$ 为AB延长线上一点，要使 $A B / / C D$ ，则可以添加的一个条件是.

查看试题解析
16. 如图，已知： $∠ B + ∠ D A B = 18 0^{°}, A C$ 平分 $∠ D A B$ ，如果 $∠ C = 5 0^{°}$ ，那么 $∠ B =$ .

查看试题解析

三、解答题（本大题共9小题，共72分）

17. 如图，已知直线AB、CD相交于点O，OE平分 $∠ A O D$ ，若 $∠ A O C = 5 0^{°}$ ，求 $∠ B O E$ 的大小．

查看试题解析
18. 如图，已知CD平分 $∠ A C B, ∠ 4 = ∠ B$ ，求证： $∠ 1 = ∠ 2$ ．

查看试题解析
19. 如图，直线AB，CD相交于点 $O, O F ⊥ C D$ ，垂足为 $O$ ，且OC平分 $∠ B O E$ ．若 $∠ A O F = 6 0^{°}$ ，求 $∠ A O E$ 的大小．

查看试题解析
20. 如图，已知 $A D ⊥ B C$ 于点D，E是延长线BA上一点，且 $E C ⊥ B C$ 于点 $C$ ，若 $∠ E = ∠ 3$ ．
求证：AD平分 $∠ B A C$ ．

查看试题解析
21. 完成下面推理过程．
在括号内、横线上填空或填上推理依据．
如图，已知： $A B / / E F, E P ⊥ E Q, ∠ E Q C + ∠ A P E = 9 0^{°}$ ，求证： $A B / / C D$ ．
证明： $∵ A B / / E F$ （已知）
$∴ ∠ A P E =$             （）
$∵ E P ⊥ E Q$ （已知）
$∴ ∠ P E Q =$             （）
即 $∠ Q E F + ∠ P E F = 9 0^{°}$
$∴ ∠ Q E F + ∠ A P E = 9 0^{°}$
$∵ ∠ E Q C + ∠ A P E = 9 0^{°}$ （已知）
$∴ ∠ E Q C =$             （）
$∴ E F / /$ （）
$∴ A B / / C D$ （平行于同一条直线的两条直线互相平行或如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．

查看试题解析
22. 如图，直线AB、CD相交于点O，OM⊥AB.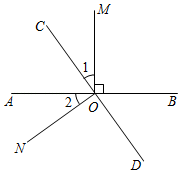

(1)、若∠1＝∠2，证明：ON⊥CD；

(2)、若∠1＝ $\frac{1}{3}$ ∠BOC，求∠BOD的度数.

查看试题解析
23. 如图， $∠ 1 + ∠ 2 = 18 0^{°}$ ．

(1)、求证： $A B / / E F$ ．

(2)、若CD平分 $∠ A C B, ∠ D E F = ∠ A, ∠ B E D = 5 0^{°}$ ，求 $∠ E D F$ 的度数．

查看试题解析
24. 综合与探究
已知 $A B / / C D, E, F$ 分别是AB，CD上的点，点 $P$ 在AB，CD之间，连接PE，PF.

(1)、如图1，若 $∠ A E P = 4 5^{°}, ∠ E P F = 8 0^{°}$ ，求 $∠ P F C$ 的度数.

(2)、如图2， $∠ A E P$ 与 $∠ C F P$ 的平分线交于点 $Q$ ，猜想 $∠ E P F$ 与 $∠ E Q F$ 之间有何数量关系?并说明理由．

(3)、如图3， $∠ A E P$ 与 $∠ C F P$ 的平分线交于点 $Q$ ，猜想 $∠ E P F$ 与 $∠ E Q F$ 之间有何数量关系?并说明理由．

查看试题解析
25. 如图1，已知直线 $A B / / E D$ ，点 $C$ 为直线AB，ED之间（不在直线上）的一个动点，连接CB，CD，BE平分 $∠ A B C, A D$ 平分 $∠ C D E, B E$ 和DA交于点 $F$ ．

(1)、证明： $∠ B A D = ∠ A D C$ ，

(2)、如图2，连接CF，则在点 $C$ 的运动过程中，当满足 $A D / / B C, C F / / A B$ 时：
①若 $∠ C F B = 5 0^{°}$ ，求 $∠ B C D$ 的度数；
②若 $∠ C F B = \frac{3}{2} ∠ D C F$ ，求 $∠ B C D$ 的度数．

查看试题解析