浙江省温州市教研院附属教育集团校2023-2024学年第二学期百基作业反馈(开学考试)九年级数学试卷
试卷更新日期:2024-04-10 类型:开学考试
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. 下列四个数中,绝对值最大的是( )A、2 B、 C、0 D、2. 某几何体如图所示,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 根据人民银行发布的《金融统计数据报告》,2023年3月末社会融资规模存量为334900000000000元,同比增长 . 将数字334900000000000用科学记数法表示为( )A、 B、 C、 D、4. 在一个不透明的袋子中装有3个红球,2个白球和4个黄球.每个球除颜色外其余均相同,从袋中随机摸出一个球,摸到红球的概率是( )A、 B、 C、 D、5. 计算的结果是( )A、 B、 C、 D、6. 已知是关于的一元二次方程的一个根,则的值为( )A、 B、 C、5 D、77. 如图是某校七年级学生参加课外兴趣小组的扇形统计图(每人只参加一项),若参加书法兴趣小组的人数是30人,则参加绘画兴趣小组的人数是( )
3. 根据人民银行发布的《金融统计数据报告》,2023年3月末社会融资规模存量为334900000000000元,同比增长 . 将数字334900000000000用科学记数法表示为( )A、 B、 C、 D、4. 在一个不透明的袋子中装有3个红球,2个白球和4个黄球.每个球除颜色外其余均相同,从袋中随机摸出一个球,摸到红球的概率是( )A、 B、 C、 D、5. 计算的结果是( )A、 B、 C、 D、6. 已知是关于的一元二次方程的一个根,则的值为( )A、 B、 C、5 D、77. 如图是某校七年级学生参加课外兴趣小组的扇形统计图(每人只参加一项),若参加书法兴趣小组的人数是30人,则参加绘画兴趣小组的人数是( ) A、36人 B、40人 C、60人 D、200人8. 如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( )
A、36人 B、40人 C、60人 D、200人8. 如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( ) A、60sin50° B、 C、60cos50° D、60tan50°9. 如图,中, , , , 经过点且半径为5的与交于 , 与的延长线交于 , 则线段的长为( )
A、60sin50° B、 C、60cos50° D、60tan50°9. 如图,中, , , , 经过点且半径为5的与交于 , 与的延长线交于 , 则线段的长为( ) A、6.4 B、7 C、7.2 D、810. 对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )A、 B、 C、 D、
A、6.4 B、7 C、7.2 D、810. 对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )A、 B、 C、 D、二、填空题(本题有6个小题,每小题4分,共24分)
-
11. 因式分解: =;12. 为了解某校九年级学生的体能情况,学校随机抽查了其中的40名学生,测试了一分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐的次数在20~30之间的频数是 .
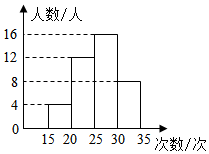 13. 不等式组的解为 .14. 一个扇形的圆心角为 , 半径为4,则该扇形的弧长为 .15. 如图,直线与轴,轴分别相交于点、 , 四边形是正方形,双曲线 在第一象限经过点 , 将正方形向下平移个单位后,点刚好落在双曲线上,则 .
13. 不等式组的解为 .14. 一个扇形的圆心角为 , 半径为4,则该扇形的弧长为 .15. 如图,直线与轴,轴分别相交于点、 , 四边形是正方形,双曲线 在第一象限经过点 , 将正方形向下平移个单位后,点刚好落在双曲线上,则 . 16. 如图,在锐角中, , , 点 , 分别在边 , 上, , 沿将翻折到 , 则的最小值为 .
16. 如图,在锐角中, , , 点 , 分别在边 , 上, , 沿将翻折到 , 则的最小值为 .
三、解答题(本题有7小题,共66分,解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算: .(2)、化简: .18. 如图,在的网格中,线段的端点都在格点上,请按要求用无刻度直尺作图.
 (1)、在图1中作点 , 使得;(2)、在图2线段上作点 , 使得:2:1.19. 为庆祝中国共产主义青年团成立102周年,学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分,成绩如图所示:
(1)、在图1中作点 , 使得;(2)、在图2线段上作点 , 使得:2:1.19. 为庆祝中国共产主义青年团成立102周年,学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分,成绩如图所示:平均数
众数
中位数
方差
八年级竞赛成绩
8
1.88
九年级竞赛成绩
8
8
1.56

根据以上信息,回答下列问题.(1)、填空: , , ;(2)、现要给成绩突出的年级颁奖,请你选择相关的统计量进行分析,应该给哪个年级颁奖?20. 如图,在平面直角坐标系中,直线的图象分别与轴,轴交于 , 两点,直线的图象分别与轴,轴交于、两点,为中点. (1)、求直线的函数解析式;(2)、直线分别与直线 , 直线交于点和点 , 当时,求的值.21. 如图,在四边形中,∥ , , 对角线、交于点 , 平分 , 过点作交延长线于点 , 连接 .
(1)、求直线的函数解析式;(2)、直线分别与直线 , 直线交于点和点 , 当时,求的值.21. 如图,在四边形中,∥ , , 对角线、交于点 , 平分 , 过点作交延长线于点 , 连接 . (1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.22. 根据以下素材,探索完成任务
(1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.22. 根据以下素材,探索完成任务研究植物叶片的生长状况
背景
素材
大自然里有许多数学的奥秘.一片美丽的心形叶片可近似看作把一条抛物线的一部分沿直线折叠而形成.

如图,建立平面直角坐标系,发现心形叶片下部轮廓线可近似看作是二次函数图象的一部分,且经过原点.

心形叶片的对称轴直线与坐标轴交于、两点,直线分别交抛物线和直线于点、点,点、是叶片上的一对对称点,交直线与点 .
问题解决
任务1
确定心形叶片的形状
求抛物线的解析式及顶点的坐标.
任务2
研究心形叶片的尺寸
求叶片此处的宽度 .
23. 如图1,在直角坐标系中,作半径为10的圆 , 交轴于点 , (点在点的左边).点为直径上一动点,过点作弦(点在点上方),连接 , 过点作∥交圆于另一点,记为点.直线交轴于点 , 连接 , , . (1)、若 , 求的度数;(2)、求证:∥;(3)、若 , 请直接写出点横坐标.
(1)、若 , 求的度数;(2)、求证:∥;(3)、若 , 请直接写出点横坐标.