浙江省宁波市镇海区蛟川书院2023-2024学年九年级(下)开学数学试卷
试卷更新日期:2024-04-10 类型:开学考试
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 若2x=5y,则的值是( )A、 B、 C、 D、2. 如图,一块矩形ABCD绸布的长AB=a,宽AD=1,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
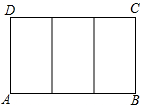 A、 B、 C、2 D、3. 如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )
A、 B、 C、2 D、3. 如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )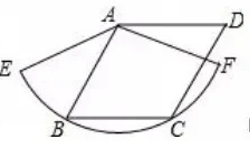 A、 B、 C、 D、4. 为测量操场上篮筐的高AB,小明站在点Q处的眼睛P与地面的距离PQ为1.7米,与AB的距离PC为2.5米,若仰角∠APC为θ,则篮筐的高AB可表示为( )
A、 B、 C、 D、4. 为测量操场上篮筐的高AB,小明站在点Q处的眼睛P与地面的距离PQ为1.7米,与AB的距离PC为2.5米,若仰角∠APC为θ,则篮筐的高AB可表示为( )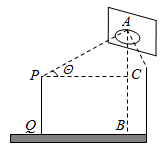 A、(1.7+2.5tanθ)米 B、(1.7+ )米 C、(1.7+2.5sinθ)米 D、(1.7+ )米5. 如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A、(1.7+2.5tanθ)米 B、(1.7+ )米 C、(1.7+2.5sinθ)米 D、(1.7+ )米5. 如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )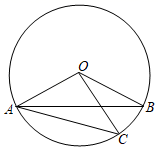 A、30° B、40° C、50° D、60°6. ⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A、30° B、40° C、50° D、60°6. ⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )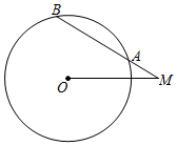 A、4 B、6 C、6 D、87. 如图,正六边形外作正方形 , 连接交于点 , 则等于( )
A、4 B、6 C、6 D、87. 如图,正六边形外作正方形 , 连接交于点 , 则等于( )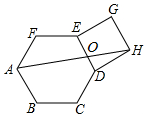 A、 B、 C、 D、8. 如图 , 一只圆形平盘被同心圆划成 , , 三个区域,随机向平盘中撒一把豆子,计算落在 , , 三个区域的豆子数的比,多次重复这个试验,发现落入三个区域的豆子数的比显示出一定的稳定性,总在三个区域的面积之比附近摆动如图将一根筷子放在该盘中位置,发现三个圆弧刚好将五等分,我们把豆子落入三个区域的概率分别记作 , , , 已知 , 则等于( )
A、 B、 C、 D、8. 如图 , 一只圆形平盘被同心圆划成 , , 三个区域,随机向平盘中撒一把豆子,计算落在 , , 三个区域的豆子数的比,多次重复这个试验,发现落入三个区域的豆子数的比显示出一定的稳定性,总在三个区域的面积之比附近摆动如图将一根筷子放在该盘中位置,发现三个圆弧刚好将五等分,我们把豆子落入三个区域的概率分别记作 , , , 已知 , 则等于( ) A、 B、 C、 D、9. 如果一个圆的内接三角形有一边的长度等于半径,那么称其为该圆的“半径三角形”给出下面四个结论:
A、 B、 C、 D、9. 如果一个圆的内接三角形有一边的长度等于半径,那么称其为该圆的“半径三角形”给出下面四个结论:一个圆的“半径三角形”有无数个;一个圆的“半径三角形”可能是锐角三角形、直角三角形或钝角三角形;当一个圆的“半径三角形”为等腰三角形时,它的顶角可能是 , 或;若一个圆的半径为 , 则它的“半径三角形”面积最大值为 .
上述结论中,所有正确结论的序号是( )
A、 B、 C、 D、10. 当时,将 , 两个点称为一对“关联的对称点”若抛物线是常数总存在一对“关联的对称点”,则的取值范围是( )A、 B、 C、 D、二、填空题:本题共6小题,每小题5分,共30分。
-
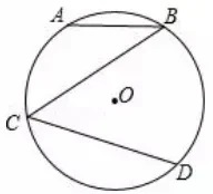
11. 二次函数的顶点坐标为12. 如图,AB、CD为 的两条弦,若 ,则 的半径为..
 13. 如图,、分别是的边、上的点, , 若:: , 则: .
13. 如图,、分别是的边、上的点, , 若:: , 则: .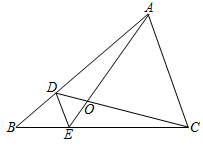 14. 如图,四边形内接于半径为的圆, , , , 则四边形的周长为 .
14. 如图,四边形内接于半径为的圆, , , , 则四边形的周长为 .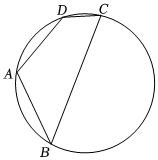 15. 贴春联是中国传统习俗,晓红老家有个圆形拱门,每年都会贴上长长的春联,看上去非常喜庆晓红用圆弧近似模拟拱门,经测量发现,的拱高和其所对的弦都是 , 所对的圆心角是 , 弦与春联的底端平齐,点正好是春联外侧最高点,则春联的外侧长度大约是参考数据 , 结果按四舍五入法精确到
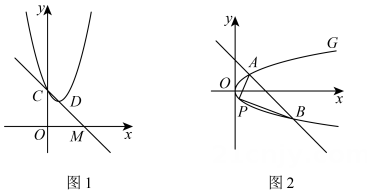
15. 贴春联是中国传统习俗,晓红老家有个圆形拱门,每年都会贴上长长的春联,看上去非常喜庆晓红用圆弧近似模拟拱门,经测量发现,的拱高和其所对的弦都是 , 所对的圆心角是 , 弦与春联的底端平齐,点正好是春联外侧最高点,则春联的外侧长度大约是参考数据 , 结果按四舍五入法精确到 16. 已知抛物线与直线相交于点 , 点在点右侧 , 且 .(1)、的值是 .(2)、直线与抛物线相交于点 , 与直线相交于点 , 若随的增大而增大,则的取值范围是 .
16. 已知抛物线与直线相交于点 , 点在点右侧 , 且 .(1)、的值是 .(2)、直线与抛物线相交于点 , 与直线相交于点 , 若随的增大而增大,则的取值范围是 .三、解答题:本题共3小题,共24分。解答应写出文字说明,证明过程或演算步骤。