浙江省温州市罗阳联盟2023-2024学年九年级下学期开学考试数学试题

试卷更新日期：2024-04-10 类型：开学考试

进入出卷网下载

一、选择题（本题有10个小题，每小题3分，共30分）

1. 2024的倒数是（）

A、 $\frac{1}{2024}$ B、2024 C、 $- 2024$ D、 $- \frac{1}{2024}$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一个正方体截去四分之一，得到如图所示的几何体，其左视图是（　　）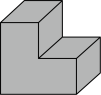

A、 B、 C、 D、

查看试题解析
4. 计算 $\frac{1}{x - 1} - \frac{2}{x^{2} - 1}$ 的结果等于（）

A、 $- 1$ B、 $x - 1$ C、 $\frac{1}{x + 1}$ D、 $\frac{1}{x^{2} - 1}$

查看试题解析
5. 如图，在平面直角坐标系中，已知 $A (2, 0)$ ， $B (4, 3)$ ， $D (5, 0)$ ， △ABC与△DEF位似，原点O是位似中心，则E点的坐标是（）

A、 $(10, 7.5)$ B、 $(8, 7)$ C、 $(10, 7)$ D、 $(8, 6)$

查看试题解析
6. 如图， $E F 、 C D$ 是 $⊙ O$ 的两条直径， $A$ 是劣弧 $\overset{⌢}{D F}$ 的中点，若 $∠ E O D = 32 °$ ，则 $∠ C D A$ 的度数是（）

A、 $37 °$ B、 $74 °$ C、 $53 °$ D、 $63 °$

查看试题解析
7. 如图，P为⊙O外一点，PA、PB分别切⊙O于点A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝6，则△PCD的周长为（）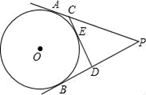

A、8 B、6 C、12 D、10

查看试题解析
8. 如图，四边形ABCD是矩形，点E、F是矩形ABCD外两点，AE⊥CF于H，AD=3，DC=4，DE= $\frac{5}{2}$ ，∠EDF=90°，则DF的长是（）

A、 $\frac{10}{3}$ B、 $\frac{11}{3}$ C、 $\frac{15}{8}$ D、 $\frac{16}{5}$

查看试题解析
9. 已知y=ax²+bx+3（a≠0）的对称轴为直线x=2，与x轴的其中一个交点为（1，0），该函数在1≤x≤4的取值范围，下列说法正确的是（）．

A、有最小值0，有最大值3 B、有最小值-1，有最大值3 C、有最小值-3，有最大值4 D、有最小值-1，有最大值4

查看试题解析
10. 如图所示是一株美丽的“勾股树”的基本图，它由3个正方形和直角三角形构成（AC＜BC）．其中∠ACB=90°，D，E分别为小正方形边的中点，两小正方形分别沿DC，CE折叠，分别记两阴影部分的面积为S₁ ， S₂ ，如图所示，当CF//AB时，S₁=3时，则S₂的值为（）

A、4 B、5 C、 $\frac{25}{9}$ D、 $\frac{16}{3}$

查看试题解析

二、填空题（共6小题，每小题4分，共24分）

11. 在“讲政策、讲法制、讲道德、讲恩情”的演讲比赛中，五位选手的成绩如下：
这组成绩的中位数是分.
选手编号
1
2
3
4
5
成绩（分）
85
92
90
95
88

查看试题解析
12. 已知tan（α+15°）＝ $\sqrt{3}$ ，则tanα的值为．

查看试题解析
13. 不透明的盒子放有三张大小、形状及质地相同的卡片，卡片上分别写有李白《峨眉山月歌》，李白《渡荆门送别》和王维《寄荆州张丞相》三首诗，小明从盒子中随机抽取两张卡片，卡片上诗的作者都是李白的概率．

查看试题解析
14. 如图，两个二次函数的图象，其顶点P ， Q都在x轴上，且有一水平线与两图象相交于A ， B ， C ， D四点，若 $A B = 12 ， B C = 6 ， C D = 8$ ，则 $P Q$ 的长度为．

查看试题解析
15. 如图，在平面直角坐标系中，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象经过顶点D，分别与对角线AC，边BC交于点E，F，连接EF，AF．若点E为AC的中点，△AEF的面积为2，则k的值为.

查看试题解析
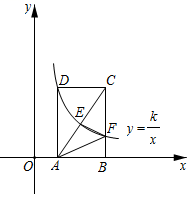16. 新能源汽车是指采用非常规的车用燃料作为动力来源，综合车辆的动力控制和驱动方面的先进技术，形成的技术原理先进、具有新技术、新结构的汽车。如图1是某新能源汽车侧面示意图，图2是该车后备箱开起侧面示意图，具体数据如图所示(单位：cm)，且AC=BD，AF//BE，sin∠BAF=0.8，箱盖开起过程中，点A，C，F不随箱盖转动，点B，D，E绕点A沿逆时针方向转动相同角度，分别到点B'，D'，E'的位置，气簧活塞杆CD随之伸长CD'.已知直线BE⊥B'E'，CD^'= $\frac{\sqrt{17}}{3}$ CD.则CD=cm

查看试题解析

三、解答题（本大题共7小题，共66分．）

17. 计算：

(1)、 ${(- \frac{1}{2})}^{- 2} + 4 c o s 30 ° - {(3 - π)}^{0} - \sqrt{12} .$

(2)、 $(a + 3) (a - 3) - a (a - 2)$ ．

查看试题解析
18. 如图，AB，DE交于点F，AD∥BE，点C在线段AB上，且AC=BE，AD=BC，连结CD，CE．

(1)、求证：△ADC≌△BCE．

(2)、若∠A=40°，∠ADC=20°，求∠CDE的度数．

查看试题解析
19. 如图，将 $△ A B C$ 放在每个小正方形的边长为1的网格中，点 $A 、 B 、 C$ 均落在格点上．

(1)、△ABC的周长等于；

(2)、点M在线段 $A B$ 上（点M与 $A 、 B$ 不重合），点N在线段 $B C$ 上（点N与 $B 、 C$ 不重合），若直线 $M N$ 恰好将△ABC的周长和面积都平分，请在如图所示的网格中，用无刻度的直尺画出直线 $M N$ .

查看试题解析
20. 某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项．现随机抽查了部分学生，并将其结果绘制成如下不完整的条形图和扇形图．
抽取的学生最喜欢体育活动的条形统计图抽取的学生最喜欢体育活动的扇形统计图
请结合以上信息解答下列问题：

(1)、在这次调查中一共抽查了学生，扇形统计图中“乒乓球”所对应的圆心角为度，并请补全条形统计图；

(2)、已知该校共有1200名学生，请你估计该校最喜爱跑步的学生人数；

(3)、若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组，请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率．

查看试题解析
21. 如图，E是菱形ABCD对角线AC上一点，四边形BGFE是矩形。点F，G分别在DC，BC上.

(1)、求证：∠CFG=∠ABE

(2)、若BE=3，tan∠ABE= $\frac{3}{4}$ 求FM的长

查看试题解析

22. 根据下列素材，完成相应任务

仓储品装容的优化设计
素材1	如图1是某个仓库，图2是其横截面的示意图，已知墙体OA=2.6米，BC=5米，水平距离OC=12米，其顶部的轮廓为抛物线的一部分，建立如图所示的平面直角坐标系后它可以近似地用函数 y= $- \frac{1}{15}$ x²+bx+c表示
素材2	图3是棱长为1m的立方体仓储品，将四件一样的仓储品如图4所示叠放在MN处，MN=1m.当叉车要取货物时，需要将其向上抬升10cm，沿水平方向移动1米后取出。
素材3	如图5，为保证能够用叉车安全顺利地搬运和放置仓储品进出仓库，需设计三条宽度为2米的过道OE，HC，FG，以及在过道之间设计两块宽度不少于2米的仓储区域EF，GH. 要求： ①靠近过道的仓储品需从就近过道搬运，其余可从左或右搬运。 ②尽可能多的装容仓储品.
问题解决
任务1	确定顶部形状	求仓库离地的最大距离.
任务2	确定摆放高度	当OM=2.4米时，试分别判断叉车能否从左边或右边取出?请说明理由。
任务3	设计最优方案	已知该仓库的长为50米，请你根据素材和要求设计：仓储区EF= ▲米， GH= ▲米，仓库最大仓储品容量为 ▲件.

查看试题解析

23. 如图1，在△ABC中， $∠ A B C = 90 °$ ， BC=1， $D$ 为 $A C$ 上一动点，连接 $B D$ ，以 $B D$ 为直径的 $⊙ O$ 交 $A B, B C, A C$ 于 $E, G, F$ ．

(1)、当 $D$ 为 $A C$ 中点时，求证： $E$ 为 $A B$ 中点；

(2)、若AB=2，连接BF，EF，当△BEF是等腰三角形时，求AD的长；

(3)、如图2，在（1）的条件下，连接 $E F$ 交 $B D$ 于 $H$ ，若 $B H = 3 D H$ ，求AB的长．

查看试题解析

选手编号	1	2	3	4	5
成绩（分）	85	92	90	95	88