湖北省黄石市2023-2024学年七年级下学期月考数学试题
试卷更新日期:2024-04-10 类型:月考试卷
一、选择题(共10小题,每小题3分,共30分.在每题给出的四个选项中,只有一个符合要求)
-
1. 下列大学校徽内部图案中可以看成由某一个基本图形通过平移形成的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,与是内错角的是( )
2. 如图,与是内错角的是( ) A、 B、 C、 D、3. 如图,要把河中的水引到水池中,应在河岸处(),开始挖渠才能使水渠的长度最短,这样做的依据是( )
A、 B、 C、 D、3. 如图,要把河中的水引到水池中,应在河岸处(),开始挖渠才能使水渠的长度最短,这样做的依据是( ) A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短4. 如图,直线与相交于点 , 若 , 则( )
A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短4. 如图,直线与相交于点 , 若 , 则( ) A、60° B、180° C、100° D、120°5. 下列命题中,正确的是( )A、两条直线被第三条直线所截,同位角相等 B、在同一平面内,平行于同一条直线的两条直线平行 C、相等的角是对顶角 D、和为180°的两个角叫做邻补角6. 含30°角的直角三角板与直线的位置关系如图所示,已知 , .则的度数是 ( )
A、60° B、180° C、100° D、120°5. 下列命题中,正确的是( )A、两条直线被第三条直线所截,同位角相等 B、在同一平面内,平行于同一条直线的两条直线平行 C、相等的角是对顶角 D、和为180°的两个角叫做邻补角6. 含30°角的直角三角板与直线的位置关系如图所示,已知 , .则的度数是 ( ) A、55° B、35° C、65° D、45°7. 如图,下列不能判定的条件是( )
A、55° B、35° C、65° D、45°7. 如图,下列不能判定的条件是( ) A、 B、 C、 D、8. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中都与地面平行, , .当为( )度时,与平行.
A、 B、 C、 D、8. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中都与地面平行, , .当为( )度时,与平行.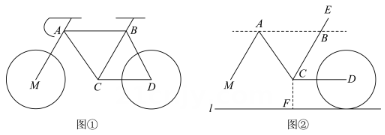 A、55 B、80 C、75 D、659. 若与的两边分别平行,且 , 则的度数为 ( )A、70° B、30° C、70°或86° D、30°或38°10. 如图, , , 若 , 则的度数为( )
A、55 B、80 C、75 D、659. 若与的两边分别平行,且 , 则的度数为 ( )A、70° B、30° C、70°或86° D、30°或38°10. 如图, , , 若 , 则的度数为( ) A、90° B、60° C、70° D、80°
A、90° B、60° C、70° D、80°二、填空题(共5小题,每小题3分,共15分)
-
11. 命题“a,b,c是直线,若a⊥b,b⊥c,则a⊥c”是 . (填写“真命题”或“假命题”)12. 如图,直线 , 则.
 13. 如图,把一张长方形纸片沿折叠后,分别落在的位置上,与交于点,若 , 则.
13. 如图,把一张长方形纸片沿折叠后,分别落在的位置上,与交于点,若 , 则.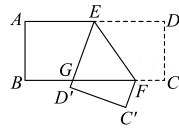 14. 已知 , 点为边上一点,过点作 , 若 , 则.15. 如图,若 , , , 则(这里均小于180°).
14. 已知 , 点为边上一点,过点作 , 若 , 则.15. 如图,若 , , , 则(这里均小于180°).
三、解答题(共9小题,共75分,解答应写出文字说明,证明过程或演算步骤)
-
16. 补全证明过程,并在( )内填写推理的依据.
已知:如图,直线被直线所截, , 求证:.
证明:

∵( ),
∴ ,
∴( ),
∵ ,
∴ ▲ ( ).
∴( ),
∴( ).
17. 如图,直线与相交于点 , 于点 , 平分 , 且 , 求的度数. 18. 如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.
18. 如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.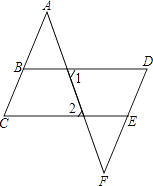 19. 已知,如图,是直线, , 求证:.
19. 已知,如图,是直线, , 求证:. 20. 如图,已知线段相交于点 , 平分 , 交于点 , .
20. 如图,已知线段相交于点 , 平分 , 交于点 , . (1)、求证:;(2)、若 , , 求的度数.21. 黄州区某酒店在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米的售价为40元,主楼梯道宽为3米,其侧面如图所示;铺设梯子的红地毯至少需要多长?花费至少多少元?
(1)、求证:;(2)、若 , , 求的度数.21. 黄州区某酒店在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米的售价为40元,主楼梯道宽为3米,其侧面如图所示;铺设梯子的红地毯至少需要多长?花费至少多少元?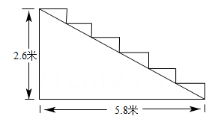 22. 图①为北斗七星的位置图,图②将北斗七星分别标为 , 将顺次首尾连接,若恰好经过点 , 且 , , .
22. 图①为北斗七星的位置图,图②将北斗七星分别标为 , 将顺次首尾连接,若恰好经过点 , 且 , , .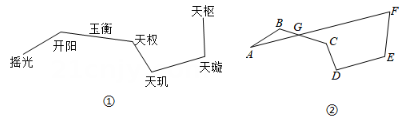 (1)、求的度数;(2)、计算的度数;(3)、连接与满足怎样数量关系时, , 并说明理由.
(1)、求的度数;(2)、计算的度数;(3)、连接与满足怎样数量关系时, , 并说明理由.