贵州省新高考协作体2023-2024学年高二(下)入学数学试卷
试卷更新日期:2024-04-10 类型:开学考试
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 已知区间 , , 则( )A、 B、 C、 D、2. 已知 , 则( )A、 B、 C、 D、3. 若函数 ( 且 )的图象经过第二、三、四象限,则一定有( ).A、 且 B、 且 C、 且 D、 且4. 已知非零复数满足为的共轭复数 , 则的模为( )A、 B、 C、 D、5. 已知双曲线的中心在坐标原点,焦点在轴上,其中一条渐近线的方程为 , 则双曲线的离心率为( )A、 B、 C、 D、6. 在中,已知 , , 则等于( )A、 B、 C、或 D、或7. 我校高二班周一有语文、数学、英语、物理、化学、体育和班会共节课,已知体育不能排在第一、二节,且数学课的前一节课不能是体育课,班会课只能在第六、七节,则该班周一的排课方法共有( )A、种 B、种 C、种 D、种8. 如图,是正四面体的内切球,球 , , , 分别是四个角处与球及正四面体的三个侧面都相切的球则球的体积与球 , , , 的体积之和的比为( )
 A、: B、: C、: D、:
A、: B、: C、: D、:二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
-
9. 已知向量 , , 则( )A、若 , 则的值为 B、与方向相同的单位向量 C、若 , 则 , D、与夹角为钝角的充要条件是10. 已知 , 为两条不同的直线, , 两个不同的平面,且 , , 则( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则11. 已知函数( , , )的部分图象如图所示,下列说法正确的是( )
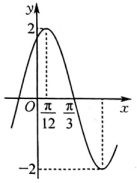 A、 B、函数为偶函数 C、函数的图象关于直线对称 D、函数在上的最小值为12. 已知定义在上的函数满足且 , 则( )A、 B、 C、为偶函数 D、为周期函数
A、 B、函数为偶函数 C、函数的图象关于直线对称 D、函数在上的最小值为12. 已知定义在上的函数满足且 , 则( )A、 B、 C、为偶函数 D、为周期函数三、填空题:本题共4小题,每小题5分,共20分。
-
13. 已知直线过点和 , 则直线的一般式方程为 .14. 已知关于的不等式的解集为 , 则实数的取值范围是 .15. 在的展开式中,含项的系数为用数字作答 .16. 已知抛物线:的焦点为 , 过点的直线与交于 , 两点,且 , 若点的坐标为 , 则的值为过点作的准线的垂线,垂足为 , 则 .
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
-
17. 近年来,某市为促进生活垃圾的分类处理、将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计生活垃圾,整理数据后得到如下统计图.
 (1)、根据统计图信息,完善下表并估计厨余垃圾投放正确的概率;
(1)、根据统计图信息,完善下表并估计厨余垃圾投放正确的概率;垃圾箱种类
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
投放量
厨余垃圾
可回收物
其他垃圾
(2)、求厨余垃圾分别在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差结果保留整数18. 已知与平面直角坐标系两坐标轴都相切的圆过点 .(1)、求圆的标准方程;(2)、若圆的半径满足其中为原点 , 且过点的直线与圆交于 , 两点,求的最小值.19. 如图,四边形为正方形,平面 , , . (1)、求证:平面;(2)、求三棱锥的体积.20. 在中,内角 , , 的对边分别为 , , , 若 .(1)、求角;(2)、若平面内一点满足 , 且 , 求面积的最大值.
(1)、求证:平面;(2)、求三棱锥的体积.20. 在中,内角 , , 的对边分别为 , , , 若 .(1)、求角;(2)、若平面内一点满足 , 且 , 求面积的最大值.
