河北省邯郸市2024届高三第三次调研考试考试数学试题

试卷更新日期：2024-04-10 类型：高考模拟

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分在每小题给出的四个选项中，只有一项是符合目要求的．

1. 已知集合 $M = {x | \sqrt{x} \leq 2}$ ， $N = {x | - 2 < x < 3}$ ，则 $M ∩ N =$ （）

A、 ${x | 0 \leq x \leq 4}$ B、 ${x | - 2 < x \leq 4}$ C、 ${x | 0 \leq x < 3}$ D、 ${x | 0 \leq x < 4}$

查看试题解析
2. 若复数 $z = \frac{a + (a - 1) i}{2 + i}$ 为纯虚数，则实数 $a =$ （）

A、 $- 2$ B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、2

查看试题解析
3. 已知向量 $\vec{a} = (m, 2)$ 与 $\vec{b} = (- 2, - 4)$ 共线，则 $3 \vec{a} - \vec{b} =$ （）

A、 $(1, 10)$ B、 $(5, 10)$ C、 $(5, 2)$ D、 $(1, 2)$

查看试题解析
4. 在 ${(x^{3} - \frac{2}{x})}^{6}$ 的展开式中， $\frac{1}{x^{2}}$ 的系数为（）

A、 $- 192$ B、 $- 6$ C、6 D、192

查看试题解析
5. 已知等比数列 ${a_{n}}$ 的各项互不相等，且 $4 a_{1}$ ， $\frac{1}{2} a_{3}$ ， $3 a_{2}$ 成等差数列，则 $\frac{a_{2021} - a_{2023}}{a_{2020} - a_{2022}} =$ （）

A、1 B、2 C、3 D、4

查看试题解析
6. 已知抛物线 $y^{2} = 8 x$ 的焦点为F ， $P (x, y)$ 为抛物线上一动点，点 $A (6, 3)$ ，则 $△ P A F$ 周长的最小值为（）

A、13 B、14 C、15 D、16

查看试题解析
7. 已知 $f (x)$ 是定义在 $R$ 上的偶函数， $f (x + 2) = f (x)$ ，且 $f (x)$ 在 $[- 1, 0]$ 上单调递减，若 $a = f (l o g_{3} 45)$ ， $b = f (- l o g_{5} 8)$ ， $c = f (\frac{4}{3})$ ，则（）

A、 $a < b < c$ B、 $a < c < b$ C、 $c < a < b$ D、 $b < c < a$

查看试题解析
8. 已知在四面体 $A B C D$ 中， $A B = B C = C D = D A = B D$ ，二面角 $A - B D - C$ 的大小为 $\frac{π}{3}$ ，且点A ， B ， C ， D都在球 $O$ 的球面上， $M$ 为棱 $A C$ 上一点， $N$ 为棱 $B D$ 的中点．若 $\vec{M O} = λ \vec{C N}$ ，则 $λ =$ （）

A、 $\frac{1}{3}$ B、 $\frac{4}{9}$ C、 $\frac{5}{9}$ D、 $\frac{2}{3}$

查看试题解析

二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. 已知双曲线 $C : \frac{x^{2}}{λ + 6} - \frac{y^{2}}{3 - λ} = 1$ ，则（）

A、 $λ$ 的取值范围是 $(- 6, 3)$ B、 $C$ 的焦点可在 $x$ 轴上也可在 $y$ 轴上 C、 $C$ 的焦距为6 D、 $C$ 的离心率 $e$ 的取值范围为 $(1, 3)$

查看试题解析
10. “阿基米德多面体”又称“半正多面体”，与正多面体类似，它们也都是凸多面体，每个面都是正多边形，并且所有棱长也都相等，但不同之处在于阿基米德多面体的每个面的形状不全相同．有几种阿基米德多面体可由正多面体进行“截角”得到如图，正八面体 $E - A B C D - F$ 的棱长为3，取各条棱的三等分点，截去六个角后得到一种阿基米德多面体，则该阿基米德多面体（）

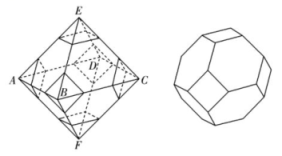A、共有18个顶点 B、共有36条棱 C、表面积为 $6 + 8 \sqrt{3}$ D、体积为 $8 \sqrt{2}$

查看试题解析
11. 已知 $△ A B C$ 的三个内角A ， B ， C的对边分别是a ， b ， c ，面积为 $\frac{\sqrt{3}}{4} (a^{2} + c^{2} - b^{2})$ ，则下列说法正确的是（）

A、 $c o s A c o s C$ 的取值范围是 $(- \frac{1}{2}, \frac{1}{4})$ B、若 $D$ 为边 $A C$ 的中点，且 $B D = 1$ ，则 $△ A B C$ 的面积的最大值为 $\frac{\sqrt{3}}{3}$ C、若 $△ A B C$ 是锐角三角形，则 $\frac{a}{c}$ 的取值范围是 $(\frac{1}{2}, 2)$ D、若角 $B$ 的平分线 $B E$ 与边 $A C$ 相交于点 $E$ ，且 $B E = \sqrt{3}$ ，则 $a + 4 c$ 的最小值为10

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分．

12. 写出一个 $ω (ω > 0)$ ，使得函数 $f (x) = s i n (2 ω x + \frac{π}{3})$ 的图象关于点 $(1, 0)$ 对称，则 $ω$ 可以为．

查看试题解析
13. 从分别写有数字1，2，3，5，9的5张卡片中任取2张，设这2张卡片上的数字之和为 $X$ ，则 $E (X) =$ ．

查看试题解析
14. 记 $m i n {x, y, z}$ 表示x ， y ， z中最小的数．设 $a > 0$ ， $b > 0$ ，则 $m i n {a, \frac{1}{b}, \frac{1}{a} + 3 b}$ 的最大值为．

查看试题解析

四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．

15. 设数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，已知 $S_{2} = 17$ ， ${\frac{S_{n}}{5 n + 7}}$ 是公差为 $\frac{1}{2}$ 的等差数列．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{1}{a_{n} a_{n + 1}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ ．

查看试题解析
16. 某民营学校为增强实力与影响力，大力招揽名师、建设校园硬件设施，近5年该校招生人数的数据如下表：
年份序号x
1
2
3
4
5
招生人数y/千人
0.8
1
1.3
1.7
2.2

(1)、由表中数据可看出，可用线性回归模型拟合 $y$ 与 $x$ 的关系，请用相关系数加以证明；

(2)、求 $y$ 关于 $x$ 的回归直线方程，并预测当年份序号为7时该校的招生人数．
参考数据： $\sum_{i = 1}^{5} x_{i} y_{i} = 24.5$ ， $\sum_{i = 1}^{5} {(y_{i} - \bar{y})}^{2} = 1.26$ ， $\sqrt{12.6} \approx 3.55$ ．
参考公式：相关系数 $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ，回归方程 $\hat{y} = b x + a$ 中斜率和截距的最小二乘估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

查看试题解析
17. 如图，在四棱锥 $P - A B C D$ 中，平面 $P C D ⊥$ 平面 $A B C D$ ， $A B / / C D$ ， $A B ⊥ B C$ ， $A B = 2 B C = 2 C D = 4$ ， $P C = 5$ ， $E$ 为棱 $A B$ 的中点，且 $C E ⊥ P E$ ．

(1)、求四棱锥 $P - A B C D$ 的高；

(2)、求二面角 $B - P C - E$ 的正弦值．

查看试题解析
18. 已知椭圆 $E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 经过 $P (- \sqrt{2}, - \frac{\sqrt{6}}{2})$ ， $Q (- 1, \frac{3}{2})$ 两点．

(1)、求 $E$ 的方程；

(2)、若圆 $x^{2} + y^{2} = 1$ 的两条相互垂直的切线 $l_{1}, l_{2}$ 均不与坐标轴垂直，且直线 $l_{1}, l_{2}$ 分别与 $E$ 相交于点A ， C和B ， D ，求四边形 $A B C D$ 面积的最小值．

查看试题解析
19. 已知函数 $f (x) = x (e^{x} - a x^{2})$ ， $a \in R$ ．

(1)、求曲线 $y = f (x)$ 在点 $(0, f (0))$ 处的切线方程．

(2)、已知关于 $x$ 的方程 $f (x) = a x^{2} - e^{x}$ 恰有4个不同的实数根 $x_{1}, x_{2}, x_{3}, x_{4}$ ，其中 $x_{1} > 0$ ， $x_{2} > 0$ ．
（i）求 $a$ 的取值范围；
（ii）求证： $x_{1} + x_{2} > 4$ ．

查看试题解析

年份序号x	1	2	3	4	5
招生人数y/千人	0.8	1	1.3	1.7	2.2