（人教版）湖南省2023-2024学年八年级下学期期中数学模拟试卷（三）

试卷更新日期：2024-04-10 类型：期中考试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{9} = \pm 3$ C、 $\sqrt{2} - \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}$ D、 $\sqrt{18} = 2 \sqrt{3}$

查看试题解析
2. 已知x，y为实数，且 $y = \frac{1}{2} + \sqrt{6 x - 1}$ $+ \sqrt{1 - 6 x} ，$ 则 $\frac{x}{y}$ 的值为（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、2

查看试题解析
3. 若式子若式子 $\frac{\sqrt{x + 2}}{x - 1}$ 有意义，则x的取值范围是（）

A、x≥-2且x≠1 B、x>-2且x≠1 C、x≥-2 D、x>-2

查看试题解析
4. 下列各组数为勾股数的是（）

A、6，12，13 B、3，4，7 C、4，7.5，8.5 D、8，15，17

查看试题解析
5. 若直角三角形两条直角边的边长分别为 $\sqrt{15}$ cm和 $\sqrt{12}$ cm，那么此直角三角形斜边长是（）

A、3 $\sqrt{2}$ cm B、3 $\sqrt{3}$ cm C、9cm D、27cm

查看试题解析
6. 如图，在数轴上，过表示数2的点A作数轴的垂线，以点A为圆心，1长为半径画弧，交垂线于点B，再以原点O为圆心，OB长为半径画弧，交数轴于点C，则点C表示的数为（）

A、2.1 B、2.2 C、 $\sqrt{5}$ D、 $\sqrt{7}$

查看试题解析
7. 如图， $△ A B C$ 是等边三角形，点 $D$ 是 $A C$ 的中点，延长 $B C$ 到点 $E$ ，使 $C E = C D = 1$ ，则 $D E$ 的长为（）

A、 $1.5$ B、 $2$ C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
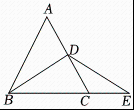8. 如图，在平面直角坐标系xOy中，四边形ABCO是平行四边形，若A，C两点的坐标分别为(3，0)，(1，2)，则▱ABCO的周长为（）

A、 $\sqrt{5}$ B、 $\sqrt{3}$ C、4 $\sqrt{5}$ D、 $6 + 2 \sqrt{5}$

查看试题解析
9. 如图，在矩形ABCD中，E，F分别是AD，BC的中点，AF 与BE，CE与DF 分别相交于点M，N，则四边形 EMFN是（）

A、正方形 B、菱形 C、矩形 D、一般的平行四边形

查看试题解析
10. 如图，在菱形ABCD中，对角线AC，BD相交于点O，E为CD的中点.若OE=3，则菱形ABCD的周长为（）

A、6 B、12 C、24 D、48

查看试题解析

二、填空题

11. 计算：

(1)、 $3 \sqrt{5} - \sqrt{5} =$ .

(2)、 $\sqrt{28} - \sqrt{7} =$ .

查看试题解析
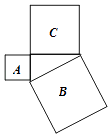
12. 已知 $a - b = - \sqrt{2} ， a b = \frac{1}{3} ，$ 则代数式 $\sqrt{a^{2} + b^{2} - 2 a b}$ $+ a^{2} + b^{2} + a b$ 的值等于 .

查看试题解析
13. 如图，正方形A、B、C的边长分别为直角三角形的三边长，若正方形A、B的边长分别为3和5，则正方形C的面积为．

查看试题解析
14. 如图，一个梯子斜靠在一竖直的墙 $A O$ 上，测得 $A O = 4 m$ ，若梯子的顶端沿墙下滑 $1 m$ ，这时梯子的底端也向右滑 $1 m$ ，则梯子 $A B$ 的长度为.

查看试题解析
15. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上， EF⊥AB，OG∥EF，AD=10，EF=4，则BG的长为.

查看试题解析
16. 如图，在▱ABCD中，若AB=4，BC=6，AC的垂直平分线交AD于点E，连结CE，则△CDE的周长为.

查看试题解析

三、解答题

17. 先化简，再求值 $\frac{a^{2} - 2 a b + b^{2}}{a - b} + (\frac{1}{b} - \frac{1}{a}) ，$ 其中a $= \sqrt{2} - 1 ， b = \sqrt{2} + 1 .$

查看试题解析
18. 高空抛物严重影响人们的安全，即便是常见的小物件，一旦从高空落下，也会产生很大的破坏性，而且坠物落地时间很短，常常避之不及.据研究，高空抛物下落的时间t(s)和高度h(m)近似满足公式 $t = \frac{\sqrt{2 h}}{g}$ 不考虑风速的影响，g≈10m/s²).

(1)、求某物体从40 m(约13层楼)高处掉落到地上所用的时间(结果保留根号).

(2)、已知高空抛物动能(单位：J)=10×物体质量(单位：kg)×高度(单位：m)，某质量为0.2kg的玩具在高空被抛出后经过 4s落在地上，假设在玩具即将落地时有行人经过，那么这个玩具产生的动能会伤害到行人吗? 请说明理由(注：无防护人体受到65 J 的动能即会受到伤害).

查看试题解析
19. 已知 $△ A B C$ 的三边长分别为 $a$ ， $b$ ， $c$ ．

(1)、化简： $\sqrt{(a - b - c)^{2}}$ ；

(2)、若 $a$ ， $b$ 满足 $b = \sqrt{5 - a} + \sqrt{a - 5} + 13$ ，且 $c = 12$ ，判断此三角形的形状，并说明理由．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B C = 4 \sqrt{2}$ ， $A B = 3 A C$ ，求AC的长.

查看试题解析
21. 如图，有两根长杆隔河相对，一杆高3m，另一杆高2m，两杆相距5m．两根长杆都与地面垂直，现两杆顶部各有一只鱼鹰，它们同时看到两杆之间的河面上E处浮出一条小鱼，于是同时以同样的速度飞下来夺鱼，结果两只鱼鹰同时叼住小鱼．求两杆底部距小鱼的距离各是多少米．（假设小鱼在此过程中保持不动）

查看试题解析
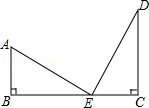22. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法，请你用等面积法来探究下列三个问题：

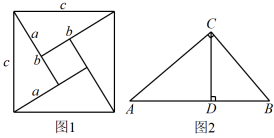(1)、如图1是著名的“赵爽弦图”，由四个全等的直角三角形拼成，请用它验证勾股定理 $c^{2} = a^{2} + b^{2}$ ．

(2)、如图2，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， C D$ 是 $A B$ 边上的高， $A C = 4 ， B C = 3$ ，求 $C D$ 的长度；

(3)、如图1，若大正方形的面积是13，小正方形的面积是1，求 ${(a + b)}^{2}$ 的值 $(a < b)$ ．

查看试题解析
23. 如图，在 ▱ ABCD中，E，F，G，H分别是AB，BC，CD，DA 上的点，且满足 AE=CG，BF=DH，连结 EG，FH.求证：EG，FH 互相平分.

查看试题解析
24. 如图，在▱ABCD中，点 E，F 在对角线 AC 上，且AE=EF=FC.

(1)、求证：四边形 DEBF 是平行四边形.

(2)、若∠CDE=90°，DC=8，DE=6，求四边形DEBF 的周长.

查看试题解析
25. 如图，在△ABC中，AB=AC，D，E分别为边AB，AC的中点，连结DE，BE，F，G，H分别为BE，DE，BC的中点，连结FG，FH.

(1)、求证：FG=FH，

(2)、若∠A=90°，求证：FG⊥FH.

(3)、若∠A=80°，求∠GFH的度数.

查看试题解析