（人教版）湖南省2023-2024学年八年级下学期期中数学模拟试卷（二）

试卷更新日期：2024-04-10 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各式是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt{- 7}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt[3]{3}$

查看试题解析
2. 下列计算错误的是（　　）

A、 $4 \sqrt{3} + 2 \sqrt{3} = 6 \sqrt{3}$ B、 $4 \sqrt{3} - 2 \sqrt{3} = 2 \sqrt{3}$ C、 $4 \sqrt{3} \div 2 \sqrt{3} = 2$ D、 $4 \sqrt{3} \times 2 \sqrt{3} = 8 \sqrt{3}$

查看试题解析
3. 代数式 $\frac{\sqrt{x + 4}}{x - 2}$ 中x的取值范围是（）

A、x≥-4 B、x>2 C、x≥-4且x≠2 D、x>-4且x≠2

查看试题解析
4. 如图所示，将一根 $24 c m$ 的筷子，置于底面直径为 $15 c m$ ，高 $8 c m$ 的圆柱形水杯中，设筷子露在杯子外面的长度 $h c m$ ，则h的取值范围是（）

A、 $h \leq 17 c m$ B、 $h \geq 8 c m$ C、 $15 c m \leq h \leq 16 c m$ D、 $7 c m \leq h \leq 16 c m$

查看试题解析
5. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（）

A、 $\sqrt{3}$ 、 $\sqrt{4}$ 、 $\sqrt{5}$ B、2、3、4 C、6、7、8 D、9、12、15

查看试题解析
6. 如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，CD⊥AB于D，则CD的长是（）

A、5 B、7 C、 $\frac{12}{5}$ D、 $\frac{24}{5}$

查看试题解析
7. 下列四组条件中，不能判定四边形ABCD为平行四边形的是（）

A、AB=CD，AD=BC B、AB∥CD，AB=CD C、AB=CD，AD∥BC D、AB∥CD，AD∥BC

查看试题解析
8. 如图，在▱ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连结AF，CE，有下列结论：①CF=AE；②OE=OF；③DE=BF；④图中共有10对全等三角形.其中正确的是（）

A、③④ B、①②③ C、①②④ D、①②③④

查看试题解析
9. 如图，在正方形ABCD中，E，F 分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP+EP最小值的是（）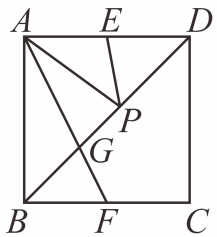

A、AB B、DG C、BD D、AF

查看试题解析
10. 如图，AC 是▱ABCD 的对角线，若当它满足：①∠1=∠2；②∠2=∠3；③∠B=∠3；④∠1=∠3 中某一条件时，▱ABCD是菱形，则这个条件是（）

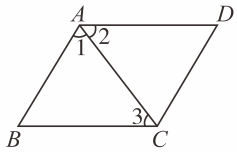A、①或② B、①或④ C、②或③ D、③或④

查看试题解析

二、填空题

11. 若式子 $\sqrt{2 x + 6}$ 在实数范围内有意义，则 $x$ 的取值范围是．

查看试题解析
12. 把 $(2 - a) \sqrt{\frac{1}{a - 2}}$ 根号外面的因式移到根号内的结果是.

查看试题解析
13. 如图，一棵树在一次强台风中在离地面 $x$ 米处折断倒下，倒下部分与地面成 $30 °$ 的夹角，树尖离树根的水平距离是 $6 \sqrt{3}$ 米，则 $x =$ ．

查看试题解析
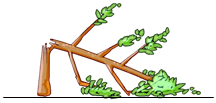14. 在△ABC中，AB＝6，AC＝5，BC边上的高AD＝4，则△ABC的周长为.

查看试题解析
15. 如图，在菱形ABCD中，对角线AC与BD相交于点O，且 $A C = 6$ ， $D B = 8$ ， $A E ⊥ B C$ 于点E，则 $A E =$ ．

查看试题解析
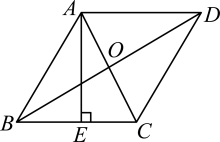16. 在 $▱$ ABCD中，已知AB=15，AC=13，BC边上的高等于12，则 $▱$ ABCD的周长是 .

查看试题解析

三、解答题

17. 若a，b为实数，且 $b = \frac{\sqrt{a^{2} - 1} + \sqrt{1 - a^{2}}}{a + 7} + 4 ，$ 求a+b的值.

查看试题解析
18. 如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡比为1 ： $\sqrt{3}$ ，求大楼AB的高度.

查看试题解析
19. 先化简，再求值： ${(\frac{a + b}{a - b})}^{2} \cdot \frac{2 a - 2 b}{3 a + 3 b} - \frac{4 a^{2}}{a^{2} - b^{2}} \div \frac{3 a}{b}$ ，其中 $a = \sqrt{3} ， b = \sqrt{2} .$

查看试题解析
20. 如图，学校有一块三角形空地 $A B C$ ，计划将这块三角形空地分割成四边形 $A B D E$ 和 $△ E D C$ ，分别摆放“秋海棠”和“天竺葵”两种不同的花卉，经测量， $∠ E D C = 90 °$ ， $D C = 3$ ， $C E = 5$ ， $B D = 7$ ， $A B = 8$ ， $A E = 1$ ，求四边形 $A B D E$ 的面积．

查看试题解析
21. 木工师傅为了让直尺经久耐用，常常在直尺的直角顶点与斜边之间加一根小木条，如左图所示，右图为其示意图．若 $∠ B A C = 90 °$ ，线段 $A B$ 的长为15cm，线段 $A C$ 的长为20cm，试求出小木条 $A D$ 的最短长度．

查看试题解析
22. 如图，有人站在离水面高度为8米的岸上A处，用绳子拉船靠岸，开始时绳子 $A B$ 的长为17米，此人以1米/秒的速度收绳，7秒后船移动到点C的位置，求此时船向岸边移动的距离是多少米（假设绳子是直的）？

查看试题解析
23. 如图，在四边形ABCD中，AB∥CD，点E，F在对角线BD上，BE=EF=FD，∠BAF=∠DCE=90°.

(1)、求证：△ABF≌△CDE.

(2)、连结AE，CF，已知 ▲ (从条件①：∠ABD=30°.条件②：AB=BC中选择一个作为已知，填序号)，请判断四边形AECF的形状，并说明理由.

查看试题解析
24. 如图，将▱ABCD的AD 边延长至点E，使 DE $= \frac{1}{2} A D ，$ 连结CE，F 是 BC 的中点，连结 FD.

(1)、求证：四边形 CEDF 是平行四边形.

(2)、若 $A B = 2 ， A D = 3 ， ∠ A = 60 ° ，$ 求CE的长.

查看试题解析
25. 如图，在 ▱ ABCD中，AF 平分∠BAD，交 BC 于点F，CE平分∠BCD，交 AD于点 E.

(1)、若AD=12，AB=8，求CF 的长.

(2)、连结 BE，与 AF 相交于点 G，连结 DF，与CE 相交于点 H，连结 EF，GH 相交于点O.求证：EF 和GH 互相平分.

查看试题解析