（人教版）湖南省2023-2024学年八年级下学期期中数学模拟试卷（一）

试卷更新日期：2024-04-10 类型：期中考试

进入出卷网下载

一、选择题

1. 已知 $0 < x < 1$ ，且 $x + \frac{1}{x} = 7$ ，则 $\sqrt{x} - \frac{1}{\sqrt{x}}$ 的值为（）

A、 $- \sqrt{10}$ B、 $- \sqrt{5}$ C、 $\sqrt{5}$ D、 $\sqrt{10}$

查看试题解析
2. 式子 $\sqrt{n + 1}$ 在实数范围内有意义，则n的取值范围为（）

A、 $n \leq - 1$ B、 $n < 1$ C、 $n \geq - 1$ D、 $n > 1$

查看试题解析
3. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{7}$ C、 $\sqrt{8}$ D、 $\sqrt{0.3}$

查看试题解析
4. 已知 $a < b$ ，且 $a b \neq 0$ ，化简二次根式 $\sqrt{- a^{3} b}$ 的结果是（）

A、 $- a \sqrt{- a b}$ B、 $- a \sqrt{a b}$ C、 $a \sqrt{a b}$ D、 $a \sqrt{- a b}$

查看试题解析
5. 若直角三角形一条直角边长为6，斜边长为10，则斜边上的高是（　　）

A、 $\frac{12}{5}$ B、 $\frac{24}{5}$ C、5 D、10

查看试题解析
6. 如图，在边长为1的正方形网格中，点A ， B ， C均在格点上，则对 $△ A B C$ 的形状描述最准确的是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形

查看试题解析
7. 如图，在赵爽弦图中，已知直角三角形的短直角边长为 $a$ ，长直角边长为 $b$ ，大正方形的面积为20，小正方形的面积为4，则 $a b$ 的值是（）

A、10 B、9 C、8 D、7

查看试题解析
8. 如图，BD为▱ABCD的对角线，∠DBC=45°，DE⊥BC于点E，BF⊥CD于点F，DE，BF相交于点H，直线BF交线段AD的延长线于点G，有下列结论：
①CE= $\frac{1}{2}$ BE；②∠A=∠BHE；③AB=BH；④∠BHD=∠BDG；⑤BH²+BG²=AG².其中正确的是（）

A、①②④ B、②③⑤ C、①⑤ D、③④

查看试题解析
9. 如图，在四边形ABCD中，AD=BC，E，F，G分别是AB，CD，AC的中点.若∠DAC=20°，∠ACB=66°，则∠FEG的度数为（）

A、18° B、21° C、22° D、23°

查看试题解析
10. 如图，在▱ABCD中，AB⊥AC.若AB=8，AC=12，则BD的长是（）

A、14 B、16 C、18 D、20

查看试题解析

二、填空题

11. 若1<x<2，则 $| x - 1 | + \sqrt{{(x - 2)}^{2}}$ 的值为.

查看试题解析
12. 若x，y为实数，且 $\sqrt{x + 3} + | y - 2 | = 0$ ，则x+y=.

查看试题解析
13. 如图，任 $R t △ A B C$ 中， $∠ C = 90 °$ ，茷 $B C = 4 ， A C = 2$ ，则 $A B$ 的长为．

查看试题解析
14. 如图， $A P$ 平分 $∠ M A N$ ， $P B ⊥ A M$ 于点 $B$ ，点 $C$ 在射线 $A N$ 上，且 $A C < A B$ ．若 $P B = 3$ ， $P C = 5$ ， $A C = 2$ ，则 $A B$ 的长为．

查看试题解析
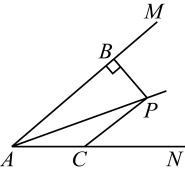15. 在边长为4的正方形ABCD中，连结对角线AC，BD，点P是正方形边上或对角线上的一点，若PB=3PC，则PC= ．

查看试题解析
16. 如图，在菱形ABCD中，AB=10cm，AC=16cm，E，F分别是CD和BC的中点，连结EP并延长与AB的延长线相交于点G，则EG的长度为cm

查看试题解析

三、解答题

17. 已知 $x = \sqrt{3} - \sqrt{7}$ ， $y = \sqrt{7} + \sqrt{3}$ ，求 ${(x + y)}^{2} - 3 x y$ 的值．

查看试题解析
18. 在解决数学问题时，有时信息不太明显，需要结合图形特殊式子成立的条件、实际问题等发现，我们把这样的条件称为隐含条件，所以我们在做题时，要注意发现题目中的隐含条件．
例如：化简( $\sqrt{1 - 3 x}$ )²-|1-x|．
解：由1-3x≥0，得x≤ $\frac{1}{3}$ ， ∴1-x>0，∴原式=(1-3x)-(1-x)=1-3x- 1+x=-2x．
按照上面的解法，试化简： $\sqrt{(x - 3)^{2}} - (\sqrt{2 - x})^{2}$ ．

查看试题解析
19. 挖掘问题中的隐含条件，解答下列问题：

(1)、已知 $\sqrt{{(x - 3)}^{2}} - {(\sqrt{2 - x})}^{2} = 2 x ，$ 求x的值.

(2)、已知a，b是实数，且 $b > \sqrt{a - 2} - 2 \sqrt{2 - a}$ +1，化简 $\sqrt{1 - 2 b + b^{2}} - \sqrt{a^{2}} ，$

查看试题解析
20. 如图，在四边形ABCD中，∠ABC=120°，AB⊥AD，BC⊥CD，AB=4，CD=5.求四边形ABCD的面积.

查看试题解析
21. 如图，在△ABC中，AB＝AC．

(1)、若P为BC上的中点，求证： $A B^{2} - A P^{2} = P B \cdot P C$ ；

(2)、若P为线段BC上的任意一点，（1）中的结论是否成立，并证明；

(3)、若P为BC延长线上一点，说明AB、AP、PB、PC之间的数量关系．

查看试题解析
22. 同学们想利用升旗的绳子、卷尺，测算学校旗杆的高度．爱动脑的小华设计了这样一个方案：如图，将升旗的绳子拉直刚好触底，此时测得绳子末端C到旗杆AB的底端B的距离为1米，然后将绳子末端拉直到距离旗杆5米的点E处，此时测得绳子末端E距离地面的高度 $D E$ 为1米．请你根据小华的测量方案和测量数据，求出学校旗杆的高度．

查看试题解析
23. 如图，在△ABC中，D，E分别为AB，AC的中点，延长DE至点F，使EF=2DE，连结FC.求证：四边形BCFE是平行四边形.

查看试题解析
24. 如图，在▱ABCD中，点E，F分别在CD，CB的延长线上，直线EF与对角线BD平行，并交AD于点H，交AB于点G.求证：EG=FH.

查看试题解析
25. 在□ABCD 中，∠ABC = 45°，对角线 AC ⊥CD.

(1)、如图1，若 AD=6，求□ABCD的面积.

(2)、如图2，连结 BD交 AC 于点O，过点 A 作AE⊥BD于点 E，连结 EC.求证：ED=AE+ $\sqrt{2}$ EC.

查看试题解析