人教版初中数学2023-2024学年八年级下学期课时培优练习19.2一次函数
试卷更新日期:2024-04-09 类型:同步测试
一、选择题
-
1. 一次函数y=(m-2)x+2-m和y=x+m在同一平面直角坐标系中的图象可能是( )A、
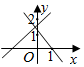 B、
B、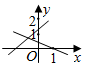 C、
C、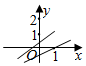 D、
D、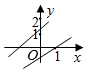 2. 若直线与直线的交点在轴上,则的值为( )A、2 B、 C、 D、3. 若直线y=kx+2与直线y=-3x+b关于直线x=-1对称,则k、b值分别为( )A、k=-3、b=-2 B、k=3、b=-2 C、k=3、b=-4 D、k=3、b=44. 一次函数与的图象如图所示,则下列说法不正确的是( )
2. 若直线与直线的交点在轴上,则的值为( )A、2 B、 C、 D、3. 若直线y=kx+2与直线y=-3x+b关于直线x=-1对称,则k、b值分别为( )A、k=-3、b=-2 B、k=3、b=-2 C、k=3、b=-4 D、k=3、b=44. 一次函数与的图象如图所示,则下列说法不正确的是( )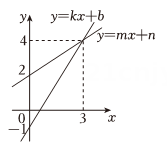 A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到35. 关于函数 , 给出下列说法正确的是:( )
A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到35. 关于函数 , 给出下列说法正确的是:( )①当时,该函数是一次函数;
②若点在该函数图象上,且 , 则;
③若该函数不经过第四象限,则;
④该函数恒过定点 .
A、①②④ B、①③④ C、②③④ D、①②③6. 已知一次函数 图象上的三点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、7. 在同一坐标系中,对于以下几个函数①;②;③ ④的图象有四种说法(1)过点的是①和③;(2)②和④的交点在y轴上;(3)互相平行的是①和③;(4)关于x轴对称的是②和③.那么正确说法的个数是( )A、4个 B、3个 C、2个 D、1个8. 已知为直线上的三个点,且 , 则下列判断中,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 如图,直线与轴交于点 , 与直线交于点 , 则关于的一元一次方程的解为( ) A、 B、 C、 D、10. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点 , , 点P是对角线OB上的一个动点, , 当最短时,点P的坐标为( )
A、 B、 C、 D、10. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点 , , 点P是对角线OB上的一个动点, , 当最短时,点P的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,直线与直线相交于点 , 则关于 , 的方程组的解是.
 12. 如图,在平面直角坐标系中,直线:与直线:交于点 , 直线与轴交于点 , 直线:过点 , 点是横轴上任意一点,满足:是等腰三角形的点坐标是 .
12. 如图,在平面直角坐标系中,直线:与直线:交于点 , 直线与轴交于点 , 直线:过点 , 点是横轴上任意一点,满足:是等腰三角形的点坐标是 .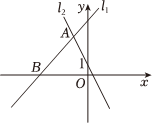 13. 在平面直角坐标系中,已知点 , , , 在直线上找一点P , 使得 , 请写出所有满足条件的点P的坐标 .14. 如图,直线 与 x 轴、y轴分别相交于A,B两点,C是OB 的中点,D是AB上一点,四边形OEDC 是菱形,则△OAE的面积为 .
13. 在平面直角坐标系中,已知点 , , , 在直线上找一点P , 使得 , 请写出所有满足条件的点P的坐标 .14. 如图,直线 与 x 轴、y轴分别相交于A,B两点,C是OB 的中点,D是AB上一点,四边形OEDC 是菱形,则△OAE的面积为 . 15. 如图,函数y=﹣5x和y=mx+3图象相交于点A(n , 2),则不等式mx+3≥﹣5x>0的解集为 .
15. 如图,函数y=﹣5x和y=mx+3图象相交于点A(n , 2),则不等式mx+3≥﹣5x>0的解集为 .
三、解答题
-
16. 在一条笔直公路上A、B两地相距120km,甲骑自行车从A地驶往B地,乙骑自行车从B地驶往A地,甲比乙先出发.设甲、乙两人距A地的路程为y(千米),甲行驶的时间为x(小时).y与x之间的关系如图所示.
 (1)、甲骑自行车的速度是千米/小时,乙骑自行车的速度是千米/小时;(2)、求乙骑自行车距A地的路程y(千米)与甲骑自行车行驶的时间x(小时)之间的函数关系式;(3)、当甲、乙两人相距20千米时,直接写出x的值.17. 如图1,已知在中, , 边在轴上,点在轴上, , 的坐标为 , 点是轴上一个动点,它的坐标是 , , 直线交直线于点 .
(1)、甲骑自行车的速度是千米/小时,乙骑自行车的速度是千米/小时;(2)、求乙骑自行车距A地的路程y(千米)与甲骑自行车行驶的时间x(小时)之间的函数关系式;(3)、当甲、乙两人相距20千米时,直接写出x的值.17. 如图1,已知在中, , 边在轴上,点在轴上, , 的坐标为 , 点是轴上一个动点,它的坐标是 , , 直线交直线于点 . (1)、求直线的表达式;(2)、若 , 点为直线上一点,且平分 , 求的坐标;(3)、如图 , 连接 , 以为直角边作等腰直角(、、三点按照逆时针顺序排列),使得 , .
(1)、求直线的表达式;(2)、若 , 点为直线上一点,且平分 , 求的坐标;(3)、如图 , 连接 , 以为直角边作等腰直角(、、三点按照逆时针顺序排列),使得 , .①试说明在点的运动过程中,的面积是否为定值,若是请求出定值,若不是请说明理由;
②点从运动到的过程中,点的运动路径长为 ▲ .
18. 如图1,已知直线与y轴交于点A , 与x轴交于点 , 直线以每秒1个单位长度的速度沿y轴正方向平移,平移时交线段于点D , 交线段于点C , 当点C与点B重合时结束运动. (1)、求k的值;(2)、若直线的函数关系式为 , P是直线上一点,当时,求点P的坐标;(3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为.当时,求t的值.19. 如图1,在平面直角坐标系中,点坐标为点坐标为是轴负半轴上一点,且是轴正半轴上一点,作于点 , 连接OD.
(1)、求k的值;(2)、若直线的函数关系式为 , P是直线上一点,当时,求点P的坐标;(3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为.当时,求t的值.19. 如图1,在平面直角坐标系中,点坐标为点坐标为是轴负半轴上一点,且是轴正半轴上一点,作于点 , 连接OD.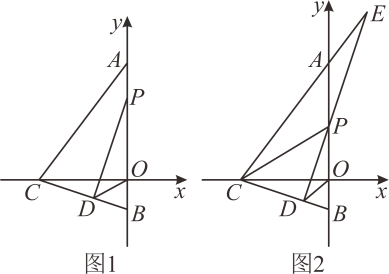 (1)、C点坐标为 , .(2)、①当点在线段OA上时,若是以OB为腰的等腰三角形,请求出所有符合条件的点坐标.
(1)、C点坐标为 , .(2)、①当点在线段OA上时,若是以OB为腰的等腰三角形,请求出所有符合条件的点坐标.②如图2,设DP交直线AC于点 , 连结CP,若 , 则 (直接写出结果).
20. 为了鼓励居民节约用水,某地区决定实行两级收费制度.若每月用水量不超过14m3(含14m3),则每立方米按政府补贴优惠价m元收费;若每月用水量超过14m3 , 则超过部分每立方米按市场价n元收费.小明家3月份用水20m3 , 缴纳水费49元;4月份用水18m3 , 缴纳水费42元.(1)、每立方米水政府补贴优惠价和市场价分别是多少?(2)、设每月用水量为x(m3),应缴纳水费为y(元),写出y关于x的函数表达式.(3)、小明家5月份用水26m3 , 则他家应缴纳水费多少元?