人教版初中数学2023-2024学年八年级下学期课时基础练习19.2一次函数
试卷更新日期:2024-04-09 类型:同步测试
一、选择题
-
1. 点、在一次函数图象上,下列结论正确的是A、 B、 C、 D、2. 点在正比例函数的图象上,则的值为( )A、 B、 C、 D、3. 已知一次函数:y= - mx +n 的图象经过第二、三、四象限,则化简 的结果是( )A、n B、-m C、2m—n D、m-2n4. 已知直线经过一、二、四象限,则直线的图象只能是( )A、
 B、
B、 C、
C、 D、
D、 5. 若 是关于 的一次函数,则 的值为( )A、 B、 C、 D、6. 在同一平面直角坐标系中,一次函数的与的图象可能是( )A、
5. 若 是关于 的一次函数,则 的值为( )A、 B、 C、 D、6. 在同一平面直角坐标系中,一次函数的与的图象可能是( )A、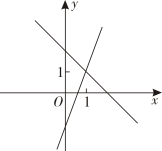 B、
B、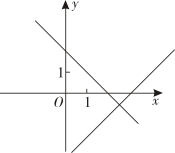 C、
C、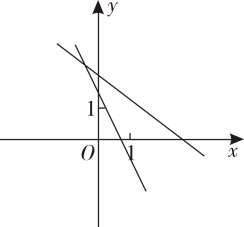 D、
D、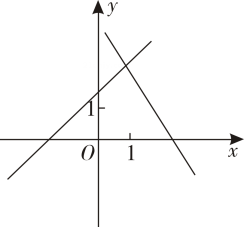 7. 如图,直线和直线相交于点 , 则方程组的解是( )
7. 如图,直线和直线相交于点 , 则方程组的解是( ) A、 B、 C、 D、8. 已知函数的图象是一条直线,下列说法正确的是( )A、直线过原点 B、随的增大而减小 C、直线经过点 D、直线经过第二、四象限9. 对于函数 , 下列说法不正确的是( )A、该函数是正比例函数 B、该函数图象过点 C、该函数图象经过一、三象限 D、随着的增大而增大10. 已知是一次函数图象上的不同的两个点,若 , 则k的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、8. 已知函数的图象是一条直线,下列说法正确的是( )A、直线过原点 B、随的增大而减小 C、直线经过点 D、直线经过第二、四象限9. 对于函数 , 下列说法不正确的是( )A、该函数是正比例函数 B、该函数图象过点 C、该函数图象经过一、三象限 D、随着的增大而增大10. 已知是一次函数图象上的不同的两个点,若 , 则k的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 一次函数y=(2m-6)x+5中,y随x的增大而减小,则m的取值范围是 .12. 将直线沿轴向上平移个单位,可得直线的解析式 .13. 若函数y=(2m+6)x+(1﹣m)是正比例函数,则m的值是 .14. 若直线经过 , 则 .15. 若一次函数的图象不经过第二象限,则k的取值范围是 .
三、解答题
-
16. 如图,直线y=x-3与x轴交于点C,与y轴交于点D,直线y=kx+b与y轴交于点B(0,4),与直线y=x-3交于点A(m,1).
 (1)、求直线AB的表达式;(2)、点P是直线CD上的一个动点,连接PB,当△PBA的面积为7时,求点P的坐标;(3)、E为y轴上的点,F在坐标平面内,以点A,B,E,F为顶点的四边形是菱形,请直接写出符合条件的点F的坐标.17. 如图,直线的图象与轴交于点 , 直线的图象与轴交于点 , 两者相交于点 .
(1)、求直线AB的表达式;(2)、点P是直线CD上的一个动点,连接PB,当△PBA的面积为7时,求点P的坐标;(3)、E为y轴上的点,F在坐标平面内,以点A,B,E,F为顶点的四边形是菱形,请直接写出符合条件的点F的坐标.17. 如图,直线的图象与轴交于点 , 直线的图象与轴交于点 , 两者相交于点 .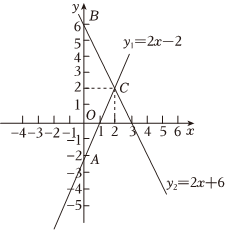 (1)、方程组的解是 ;(2)、当与同时成立时,的取值范围为 ;(3)、在直线的图象上存在异于点的另一点 , 使得与的面积相等,求出点的坐标.18. 某公司计划购买两种设备共100台,要求种设备数量不低于种的 , 且不高于种的 . 已知两种设备的单价分别是1000元/台,1500元/台,设购买种设备台.(1)、求该公司计划购买这两种设备所需费用(元)与的函数关系式;(2)、求该公司按计划购买这两种设备有多少种方案?(3)、由于市场行情波动,实际购买时,种设备单价上调了元/台,种设备单价下调了元/台,此时公司购买这两种设备所需最少费用为121500元,请直接写出的值.
(1)、方程组的解是 ;(2)、当与同时成立时,的取值范围为 ;(3)、在直线的图象上存在异于点的另一点 , 使得与的面积相等,求出点的坐标.18. 某公司计划购买两种设备共100台,要求种设备数量不低于种的 , 且不高于种的 . 已知两种设备的单价分别是1000元/台,1500元/台,设购买种设备台.(1)、求该公司计划购买这两种设备所需费用(元)与的函数关系式;(2)、求该公司按计划购买这两种设备有多少种方案?(3)、由于市场行情波动,实际购买时,种设备单价上调了元/台,种设备单价下调了元/台,此时公司购买这两种设备所需最少费用为121500元,请直接写出的值.