（人教版）湖南省2023-2024学年七年级下学期期中数学模拟试卷（二）

试卷更新日期：2024-04-09 类型：期中考试

进入出卷网下载

一、选择题

1. 已知直线AB及AB外一点P，若过点P作一直线与AB平行，那么这样的直线（）

A、有且只有一条 B、有两条 C、不存在 D、无数条

查看试题解析
2. 如图，直线a∥b，直角三角形ABC的直角顶点B落在直线a上，若∠1=25° ，则∠2的大小为（）

A、55° B、65° C、75° D、85°

查看试题解析
3. 如图，∠B+∠DCB=180°，AC平分∠DAB，且∠D：∠DAC=5：2，则∠D的度数是（）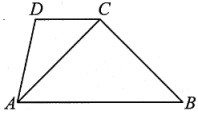

A、100° B、105° C、110° D、120°

查看试题解析
4. 下列各数中的无理数是（）

A、 $\sqrt{4}$ B、 $π$ C、0 D、 $- \frac{22}{7}$

查看试题解析
5. -8的立方根是（）

A、-2 B、2 C、±2 D、4

查看试题解析
6. 下列运算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、（﹣2）³=8 C、﹣|﹣3|=3 D、﹣2²=﹣4

查看试题解析
7. 一个正方体的水晶砖，体积为100cm³ ，它的棱长大约在（　　）

A、4cm~5cm之间 B、5cm~6cm之间 C、6cm~7cm之间 D、7cm~8cm之间

查看试题解析
8. 在平面直角坐标系 $x O y$ 中， $A (5 \sqrt{3} ， 0)$ ， $A B = 7 \sqrt{3}$ ，以点 $A$ 为圆心， $A B$ 长为半径画弧交 $x$ 轴负半轴于点 $C$ ，则点 $C$ 的坐标为（）

A、 $(- 12 \sqrt{3} ， 0)$ B、 $(- 2 \sqrt{3} ， 0)$ C、 $(0 ， - 12 \sqrt{3})$ D、 $(0 ， - 2 \sqrt{3})$

查看试题解析
9. 如图，小手盖住的点的坐标可能是（　　）．

A、（﹣3，4）； B、（5，2） C、（﹣3，﹣6）； D、（6，﹣4）．

查看试题解析
10. 在平面直角坐标系xOy中，点 $P (1 - m ， 8)$ 在第二象限，则m的取值范围是（）

A、 $m > 1$ B、 $m < 1$ C、 $m \leq 1$ D、 $m \geq 1$

查看试题解析

二、填空题

11. 如图，在长方形ABCD中，AB=10cm，BC=6cm，将长方形ABCD沿着AB方向每秒平移2 cm，则s后，才能使平移后的长方形EFGH与原来的长方形ABCD重叠部分的面积为24 cm² ．

查看试题解析
12. 如图，一把直尺沿直线断开并错位，点E，D，B，F在同一条直线上，若∠ADE=125°，则∠CBF的度数为

查看试题解析
13. 7的算术平方根是．

查看试题解析
14. 已知：若 $\sqrt{3.65}$ ≈1.910， $\sqrt{36.5}$ ≈6.042，则 $\sqrt{365000}$ ≈ ．

查看试题解析
15. 若点 $A （ 2 ， 3 m - 1 ）$ 在x轴上，点 $B （ 2 n + 1 ， 3 ）$ 在y轴上，则代数式 $6 m + 4 n$ 的值是．

查看试题解析
16. 若点 $A (m + 2 ， 2 m - 5)$ 在 $y$ 轴上，则 $m =$ ．

查看试题解析

三、解答题

17. 如图， $D$ 、 $E$ 、 $F$ 分别在 $△ A B C$ 的三条边上，且 $D E ∥ A B$ ， $∠ 1 = ∠ 2$ ．

(1)、完成下列证明：
证明： $D F ∥ A C$ ．
$∵ D E ∥ A B$ ，
$∴ ∠ A =$ ；
$∵ ∠ 1 = ∠ 2$ ，
$∴$ $=$ ；
$∴ A C ∥$ ．

(2)、若 $∠ B = 40 °$ ， $D F$ 平分 $∠ B D E$ ，求 $∠ C$ 度数．

查看试题解析
18. 如图所示，直线AE∥CD，B为AE上的点，BC平分∠ABD，∠1=65°，求∠2的度数。

查看试题解析
19. 如图，已知AB∥DE，∠1=18°，∠2=125°，求∠BCD的度数.

查看试题解析
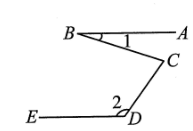20. 中国清代学者华衡芳和英国人傅兰雅合译英国瓦里斯的《代数学》，卷首有“代数之头，无论何数，皆可以任何记号代之”，说明了所谓“代数”，就是和符号来代表数的一种方法，若一个正数的平方根分别是 $2 a - 3$ 和 $5 - a$ ，求这个正数．

查看试题解析
21. 已知x是 $- 64$ 的立方根，y的算术平方根是 $\sqrt{13}$ ，求 $x + y$ 的平方根．

查看试题解析
22. 一个正方体的体积是16，另一正方体的体积是这个正方体体积的4倍，求另一个正方体的表面积．

查看试题解析
23. 已知点 $A (3 a - 9 ， 2 a - 10)$ ，解答下列问题：

(1)、若点 $B$ 的坐标为 $(4 ， 5)$ ，且 $A B / / y$ 轴，求 $a$ 的值；

(2)、若点 $A$ 在第四象限，且 $a$ 是整数，求点 $A$ 的坐标．

查看试题解析
24. 如图所示的是某市区几个旅游景点的示意图（图中每个小正方形的边长为1个单位长度），若海洋极地公园的坐标为（4，0），大唐芙蓉园的坐标为（2，-1），请建立平面直角坐标系，并用坐标表示其他景点的位置．

查看试题解析
25.
在平面直角坐标系中，点O是坐标原点，点A的坐标是（-a，a），点B的坐标是（c，b），满足 ${\begin{cases} 3 a - b + 2 c = 8 \\ a - 2 b - c = - 4 \end{cases}$ .

(1)、a为不等式2x+6<0的最大整数解，求a的值并判断点A在第几象限；

(2)、在（1）的条件下，求△AOB的面积；

(3)、在（2）的条件下，若两个动点M（k-1，k），N（-2h+10，h），请你探索是否存在以两个动点M、N为端点的线段MN//AB，且MN=AB，若存在，求M、N两点的坐标；若不存在，请说明理由.

查看试题解析