人教版初中数学2023-2024学年八年级下学期课时培优练习19.1变量与函数
试卷更新日期:2024-04-09 类型:同步测试
一、选择题
-
1. 如图,在一个内角为60°的菱形 ABCD中,AB=2,点P以每秒1cm的速度从点A出发,沿AD→DC的路径运动,到点C停止,过点P 作PQ⊥BD,PQ 与边AD(或边CD)交于点Q,△ABQ的面积y(cm2)与点P 的运动时间x(秒)的函数图象大致是( )
 A、
A、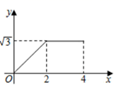 B、
B、 C、
C、 D、
D、 2. 某种型号的计算器单价为40元,商家为了扩大销售量,现按八折销售,如果卖出x台这种计算器,共卖得y元,则用x表示y的关系式为( )A、y=40x B、y=32x C、y=8x D、y=48x3. 甲、乙两地相距千米,一辆货车和一辆轿车分别从甲地开往乙地轿车的平均速度大于货车的平均速度 , 如图线段和折线分别表示两车离甲地的距离单位:千米与时间单位:小时之间的函数关系则下列说法正确的是( )
2. 某种型号的计算器单价为40元,商家为了扩大销售量,现按八折销售,如果卖出x台这种计算器,共卖得y元,则用x表示y的关系式为( )A、y=40x B、y=32x C、y=8x D、y=48x3. 甲、乙两地相距千米,一辆货车和一辆轿车分别从甲地开往乙地轿车的平均速度大于货车的平均速度 , 如图线段和折线分别表示两车离甲地的距离单位:千米与时间单位:小时之间的函数关系则下列说法正确的是( ) A、两车同时到达乙地 B、轿车在行驶过程中的平均速度为千米小时 C、货车出发小时后,轿车追上货车 D、两车在前千米的速度相等4. 某油箱容量为的汽车,加满汽油后开了时,油箱中的汽油大约消耗了四分之一,如果加满汽油后汽车行驶的路程为 , 油箱中的剩油量为 , 则与之间的函数解析式和自变量取值范围分别是( )A、 , B、 , C、 , D、 ,5. 在函数中,自变量x的取值范围是( )A、 B、且 C、 D、且6. 若等腰三角形的周长为60 cm,底边长为x cm,一腰长为y cm,则y关于x的函数解析式及自变量x的取值范围是( )A、y=60-2x(0<x<60) B、y=60-2x(0<x<30) C、y= (60-x)(0<x<60) D、y= (60-x)(0<x<30)7. 学校离小林家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,然后又行驶了5分钟到家,在下列图形中能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的函数关系是( )A、
A、两车同时到达乙地 B、轿车在行驶过程中的平均速度为千米小时 C、货车出发小时后,轿车追上货车 D、两车在前千米的速度相等4. 某油箱容量为的汽车,加满汽油后开了时,油箱中的汽油大约消耗了四分之一,如果加满汽油后汽车行驶的路程为 , 油箱中的剩油量为 , 则与之间的函数解析式和自变量取值范围分别是( )A、 , B、 , C、 , D、 ,5. 在函数中,自变量x的取值范围是( )A、 B、且 C、 D、且6. 若等腰三角形的周长为60 cm,底边长为x cm,一腰长为y cm,则y关于x的函数解析式及自变量x的取值范围是( )A、y=60-2x(0<x<60) B、y=60-2x(0<x<30) C、y= (60-x)(0<x<60) D、y= (60-x)(0<x<30)7. 学校离小林家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,然后又行驶了5分钟到家,在下列图形中能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的函数关系是( )A、 B、
B、 C、
C、 D、
D、 8. 下列函数关系式中,自变量x的取值范围不正确的是( )A、y=2x2中,x为全体实数 B、y=中,x≠﹣1 C、y=中,x=0 D、y=中,x>﹣79. 若定义一种新运算: , 例如:; . 则函数的图象大致是( )A、
8. 下列函数关系式中,自变量x的取值范围不正确的是( )A、y=2x2中,x为全体实数 B、y=中,x≠﹣1 C、y=中,x=0 D、y=中,x>﹣79. 若定义一种新运算: , 例如:; . 则函数的图象大致是( )A、 B、
B、 C、
C、 D、
D、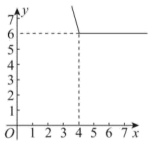 10. 一次函数 ,若 ,则它的图象必经过点( )A、 B、 C、 D、
10. 一次函数 ,若 ,则它的图象必经过点( )A、 B、 C、 D、二、填空题
-
11. 如果直线经过点 , 那么关于x的方程的解是 .12. 根据如图的程序计算,当输入时,输出的结果y=;当输出的结果时,则输入x= .
 13. 已知变量x,y满足 ,那么 与 之间的函数关系式为.14. 函数 中x的取值范围是.15. 小明参加了步行活动中,中途休息了一段时间.设他从学校出发后所用时间为 (分钟),所走的路程为 (米 ,s与t之间的函数关系如图17所示.则下列说法中,正确的序号为 .
13. 已知变量x,y满足 ,那么 与 之间的函数关系式为.14. 函数 中x的取值范围是.15. 小明参加了步行活动中,中途休息了一段时间.设他从学校出发后所用时间为 (分钟),所走的路程为 (米 ,s与t之间的函数关系如图17所示.则下列说法中,正确的序号为 .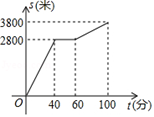
①小明中途休息用了20分钟.
②小明休息前步行的平均速度为每分钟70米.
③小明休息前步行的平均速度大于休息后步行的平均速度.
④小明行走的路程为6600米.
三、解答题
-
16. 枣庄某公交车每天的支出费用为元,每天的乘车人数人与每天利润利润票款收入支出费用元的变化关系,如下表所示每位乘客的乘车票价固定不变:
人
元
根据表格中的数据,回答下列问题:
(1)、 是自变量;(2)、观察表中数据可知,当乘客量达到 人以上时,该公交车才不会亏损;(3)、请写出公交车每天利润元与每天乘车人数人的关系式: ;(4)、当一天乘客人数为多少人时,利润是元?四、综合题
-
17. 在“看图说故事”活动中,某学习小组结合图像设计了一个问题情境.

已知小明家、食堂、图书馆依次在同一条直线上.食堂离小明家 . 图书馆离小明家 . 周末,小明从家出发,匀速走了到食堂;在食堂停留吃早餐后,匀速走了到图书馆;在图书馆读报停留 , 然后匀速走了返回家.给出的图像反映了这个过程中小明离家的距离与离开家的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:小明离开家的时间/min
8
20
40
小明离家的距离/km
(2)、填空:①食堂到图书馆的距离为km;
②小明从图书馆返回家中的速度为;
③当小明离家的距离为时,他离开家的时间为min.
(3)、当时,请直接写出y关于x的函数解析式.18. 大同市拥有完善的能源、重工业产业体系,是国内重要的煤化工、矿山机械等产业基地,具有较强的产业基础和技术优势,本市某企业的一个生产组有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润180元,在这10名工人中,车间每天安排名工人生产甲种产品,其余工人生产乙种产品.(1)、求出此车间每天获取利润(元)与(人)之间的函数解析式;(2)、若要使此车间每天获取利润不低于15600元,你认为最多派多少名工人去生产甲种产品才合适?19. 有这样一个问题:探究函数的图象与性质.小亮根据学习函数的经验,对的图象与性质进行了探究:下面是小亮的探究过程,请补充完整:
(1)、函数中自变量x的取值范围是;(2)、下表是y与x的几组对应值.x
…
y
…
0
1
m
…
求得表中m的值为 ;
(3)、在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点.并结合对函数解析式分析,画出该函数的图象: (4)、根据画出的函数图象,发现下列特征:
(4)、根据画出的函数图象,发现下列特征:①该函数的图象与直线越来越靠近而永不相交,该函数的图象还与直线 越来越靠近而永不相交,因此因变量y的取值范围是 .
②写出该函数的增减性为 .
20. 如图:在中, , 高 , 动点P由点C沿向点B运动(不与点B重合),设的长为x , 的面积为S . (1)、在这个过程中,常量有变量有(2)、请写出S与x之间的函数关系式,并指出自变量x的取值范围(3)、当x取时计算此时的S值(4)、S为时,求出对应x的值
(1)、在这个过程中,常量有变量有(2)、请写出S与x之间的函数关系式,并指出自变量x的取值范围(3)、当x取时计算此时的S值(4)、S为时,求出对应x的值
-