(人教版)贵州省2023-2024学年八年级下学期期中数学模拟试卷(一)
试卷更新日期:2024-04-09 类型:期中考试
一、选择题
-
1. 二次根式中,x的取值范围是( )A、 B、 C、 D、2. 已知最简二次根式 与 是同类二次根式,则a的值是( )A、2 B、3 C、4 D、53. 若 , 则等于( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为( )
 A、6 B、36 C、64 D、86. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3 , EF=3,则FN的长为( )
A、6 B、36 C、64 D、86. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3 , EF=3,则FN的长为( ) A、2 B、 C、 D、37. 下列各组数中,属于勾股数的是( )A、 , , B、 , , C、 , , D、 , ,8. 在中, , , 则( )A、 B、 C、 D、或9. 如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A、2 B、 C、 D、37. 下列各组数中,属于勾股数的是( )A、 , , B、 , , C、 , , D、 , ,8. 在中, , , 则( )A、 B、 C、 D、或9. 如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )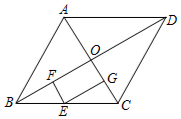 A、 B、 C、 D、10. 如图,为正方形对角线的中点,为等边三角形.若 , 则的长度为( )
A、 B、 C、 D、10. 如图,为正方形对角线的中点,为等边三角形.若 , 则的长度为( ) A、 B、 C、 D、11. 如图,若菱形的周长 , 则菱形的一边的中点E到对角线交点O的距离为( )
A、 B、 C、 D、11. 如图,若菱形的周长 , 则菱形的一边的中点E到对角线交点O的距离为( )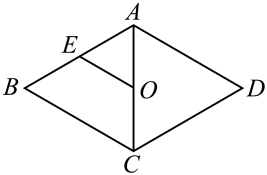 A、 B、 C、 D、12. 如图,平行四边形的对角线 , 交于点 , 已知 , , 的周长为15,则的长为( )
A、 B、 C、 D、12. 如图,平行四边形的对角线 , 交于点 , 已知 , , 的周长为15,则的长为( ) A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
13. 实数a,b在数轴上的位置如图所示,化简|a+1|- = .
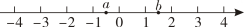 14. 如图, , , , 点在点的北偏西方向,则点在点的方向.
14. 如图, , , , 点在点的北偏西方向,则点在点的方向.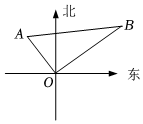 15. 已知a=2,则16. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .
15. 已知a=2,则16. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .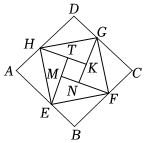
三、解答题
-
17. 若a,b为实数,且b= , =a+3,求ab+c的值18.(1)、已知 , 求代数式 的值.(2)、 已知 求代数式 的值.19. 某居民小区有一块形状为长方形的绿地ABCD,长方形绿地的长BC为 m,宽AB为 m,现要在长方形绿地中修建一个长方形 花坛(即图中阴影部分),长方形花坛的长为( +1)m,宽为( -1)m.
 (1)、长方形ABCD的周长是多少?(2)、除去修建花坛的地方,其他地方全修建成通道,通道上要铺上造价为5元/m2的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)20. 如图,是等腰三角形, , 点是边上的一点,连接 .
(1)、长方形ABCD的周长是多少?(2)、除去修建花坛的地方,其他地方全修建成通道,通道上要铺上造价为5元/m2的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)20. 如图,是等腰三角形, , 点是边上的一点,连接 .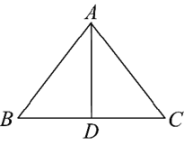 (1)、若的周长是 , , 点是的中点,求的长;(2)、若 , , , 求的面积.21. 如图,在和中, , , , 延长 , 交于点M .
(1)、若的周长是 , , 点是的中点,求的长;(2)、若 , , , 求的面积.21. 如图,在和中, , , , 延长 , 交于点M . (1)、求证:平分;(2)、若 , , , 求的长.22. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米.
(1)、求证:平分;(2)、若 , , , 求的长.22. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米. (1)、求这块空地的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?23. 如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
(1)、求这块空地的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?23. 如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF. (1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.24. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,A(-3,0),B(3,0) ,C(0,4),连结OD,点E是线段0D的中点.
(1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.24. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,A(-3,0),B(3,0) ,C(0,4),连结OD,点E是线段0D的中点. (1)、求点E和点D的坐标.(2)、平面内是否存在一点N,使以C,D,E,N为顶点的四边形是平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.25. 如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F.
(1)、求点E和点D的坐标.(2)、平面内是否存在一点N,使以C,D,E,N为顶点的四边形是平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.25. 如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F. (1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.