(人教版)贵州省2023-2024学年七年级下学期期中数学模拟试卷(一)
试卷更新日期:2024-04-09 类型:期中考试
一、选择题
-
1. 如图,将一张长方形纸对折两次,产生的折痕与折痕之间的位置关系是( )
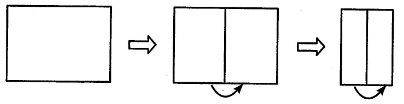 A、平行 B、垂直 C、平行或垂直 D、无法确定2. 如图,直线与相交于点 , 平分 , 且 , 则为( )
A、平行 B、垂直 C、平行或垂直 D、无法确定2. 如图,直线与相交于点 , 平分 , 且 , 则为( )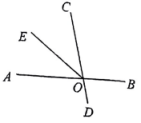 A、 B、 C、 D、3. 如图,把一块含有30°角的三角尺的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数是( )
A、 B、 C、 D、3. 如图,把一块含有30°角的三角尺的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数是( ) A、22° B、32° C、38° D、44°4. 如图,已知AB∥CD,∠C=80°,则∠A等于( )
A、22° B、32° C、38° D、44°4. 如图,已知AB∥CD,∠C=80°,则∠A等于( ) A、80° B、100° C、110° D、120°5. 平方根等于它本身的数是( )A、0 B、 C、1 D、6. 9的算术平方根是( )A、±3 B、﹣3 C、3 D、±817. 下列计算正确的是( )A、 B、 C、 D、8. 在 , , , ,2023这五个数中无理数的个数为( )A、2 B、3 C、4 D、59. 在平面直角坐标系中,横、纵坐标都是整数的点称为整点,已知 , , n为正整数,且线段AB上共有2024个整点,则n的值是( )A、1348 B、1349 C、1011 D、101210. 如果点的坐标满足 , 那么称点为“美丽点”,若某个“美丽点”到轴的距离为 , 则点的坐标为( )A、 B、 C、或 D、或11. 如图,将线段平移到线段的位置,则的值为( )
A、80° B、100° C、110° D、120°5. 平方根等于它本身的数是( )A、0 B、 C、1 D、6. 9的算术平方根是( )A、±3 B、﹣3 C、3 D、±817. 下列计算正确的是( )A、 B、 C、 D、8. 在 , , , ,2023这五个数中无理数的个数为( )A、2 B、3 C、4 D、59. 在平面直角坐标系中,横、纵坐标都是整数的点称为整点,已知 , , n为正整数,且线段AB上共有2024个整点,则n的值是( )A、1348 B、1349 C、1011 D、101210. 如果点的坐标满足 , 那么称点为“美丽点”,若某个“美丽点”到轴的距离为 , 则点的坐标为( )A、 B、 C、或 D、或11. 如图,将线段平移到线段的位置,则的值为( )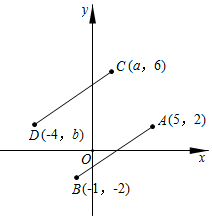 A、 B、 C、 D、12. 已知点Q的坐标为 ,点P的坐标为 ,若直线 轴,则点P的坐标为( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知点Q的坐标为 ,点P的坐标为 ,若直线 轴,则点P的坐标为( )A、 B、 C、 D、二、填空题
-
13. 有经验的渔夫用鱼叉捕鱼时,不是将鱼叉对准他看到的鱼,这是由于光从空气射入水中时,发生折射现象.如图,水面与底面平行,光线从空气射入水中时发生了折射,变成光线射到水底处,射线是光线的延长线, , , 则的度数为 .
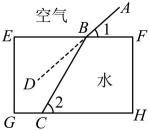 14. 如图,直线 , 直线与相交,若 , 则 .
14. 如图,直线 , 直线与相交,若 , 则 .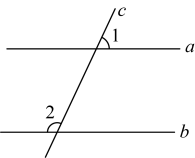 15. 比较大小:4.16. 若点在x轴上,则 .
15. 比较大小:4.16. 若点在x轴上,则 .三、解答题
-
17. 如图,点在直线上, , .
 (1)、若 , 求的度数;(2)、试猜想和的数量关系,请直接写出结果 .18. 如图,AB∥CD,EF分别交AB,CD于点M,N,∠1=52°,MG平分∠BMF交CD于点G,求∠2的度数.
(1)、若 , 求的度数;(2)、试猜想和的数量关系,请直接写出结果 .18. 如图,AB∥CD,EF分别交AB,CD于点M,N,∠1=52°,MG平分∠BMF交CD于点G,求∠2的度数.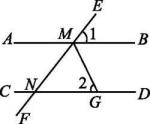 19. 如图,AD∥BC,∠B=∠D=40°,点E,F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.
19. 如图,AD∥BC,∠B=∠D=40°,点E,F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.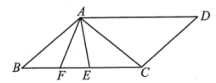 (1)、∠CAF= .(2)、若平行移动CD,其余条件不变,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.20. 一个正数x的两个不同的平方根分别是和 .(1)、求a和x的值;(2)、化简:21. 据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊讶,忙问计算的奥秘.你知道华罗庚是怎样迅速准确地计算出来的吗?请按照下面的问题试一试:(1)、由 , , 可以确定是位数,由59319的个位上的数是9,可以确定的个位上的数字是 , 如果划去59319后面的三位319得到数59,而 , , 由此可以确定的十位上的数字是;(2)、已知32768,-274625都是整数的立方,按照上述方法,请你分别求它们的立方根.22. 如图,在平面直角坐标系中,将点向右平移到点 , 以为边在下方作正方形 .
(1)、∠CAF= .(2)、若平行移动CD,其余条件不变,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.20. 一个正数x的两个不同的平方根分别是和 .(1)、求a和x的值;(2)、化简:21. 据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊讶,忙问计算的奥秘.你知道华罗庚是怎样迅速准确地计算出来的吗?请按照下面的问题试一试:(1)、由 , , 可以确定是位数,由59319的个位上的数是9,可以确定的个位上的数字是 , 如果划去59319后面的三位319得到数59,而 , , 由此可以确定的十位上的数字是;(2)、已知32768,-274625都是整数的立方,按照上述方法,请你分别求它们的立方根.22. 如图,在平面直角坐标系中,将点向右平移到点 , 以为边在下方作正方形 . (1)、求的值及点的坐标;(2)、横、纵坐标都是整数的点叫做整点.已知点 , , 将正方形向左平移个单位长度,得到正方形 , 记正方形和重叠的区域(不含边界)为 .
(1)、求的值及点的坐标;(2)、横、纵坐标都是整数的点叫做整点.已知点 , , 将正方形向左平移个单位长度,得到正方形 , 记正方形和重叠的区域(不含边界)为 .①当时,区域内的整点个数为 ▲ 个;
②若区域内恰有3个整点,请直接写出这3个整点坐标和对应的取值范围.
23. 如图,在平面直角坐标系中, , 点在x轴的负半轴上,点C在第二象限,轴,且 , 点在第一象限.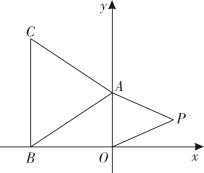 (1)、求B , C两点的坐标;(2)、是否存在m , 使以A , B , O , P为顶点的四边形的面积等于?若存在,求出点P的坐标,若不存在,请说明理由.24. 先阅读下面的文字,然后解答问题.
(1)、求B , C两点的坐标;(2)、是否存在m , 使以A , B , O , P为顶点的四边形的面积等于?若存在,求出点P的坐标,若不存在,请说明理由.24. 先阅读下面的文字,然后解答问题.大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:如果 , 其中是整数,且 , 那么 , .请解答下列问题:
(1)、如果 , 其中a是整数,且 , 那么 , b=;(2)、已知 , 其中m是整数,且 , 求的值;(3)、的整数部分是 , 小数部分是.