(人教版)云南省2023-2024学年八年级下学期期中数学模拟试卷(三)
试卷更新日期:2024-04-09 类型:期中考试
一、选择题
-
1. 若成立,则x的值可以是( )A、-2 B、0 C、2 D、32. 下列计算正确的是( )A、 B、 C、 D、3. 下列二次根式中与 是同类二次根式的是( )A、 B、 C、 D、4. 已知 ,则 的值为( )A、 B、 C、 D、5. 下列图各组数中,是勾股数的是( )A、6,8,12 B、0.6,0.8,1 C、8,15,16 D、9,12,156. 如图,在中, , 分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线 , 分别交、于点、 , 连接 , 则的面积为( )
 A、 B、 C、 D、7. 如图,在中, , 在数轴上,点所表示的数为1,以点为圆心,长为半径画弧,在点左侧交数轴于点 , 则点表示的数是( )
A、 B、 C、 D、7. 如图,在中, , 在数轴上,点所表示的数为1,以点为圆心,长为半径画弧,在点左侧交数轴于点 , 则点表示的数是( ) A、 B、 C、 D、8. 成书于大约公元前1世纪的《周髀算经》是中国现存最早的一部数学典籍,里面记载的勾股定理的公式与证明相传是在西周由商高发现,故又称之为商高定理.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1;古希腊哲学家柏拉图(公元前427年—公元前347年)研究了勾为( , m为正整数),弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为12,则其股为( )
A、 B、 C、 D、8. 成书于大约公元前1世纪的《周髀算经》是中国现存最早的一部数学典籍,里面记载的勾股定理的公式与证明相传是在西周由商高发现,故又称之为商高定理.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1;古希腊哲学家柏拉图(公元前427年—公元前347年)研究了勾为( , m为正整数),弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为12,则其股为( ) A、14 B、16 C、35 D、379. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形10. 如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE⊥AC于E,PF⊥BC于点F,连结EF,则线段EF的最小值为( )
A、14 B、16 C、35 D、379. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形10. 如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE⊥AC于E,PF⊥BC于点F,连结EF,则线段EF的最小值为( ) A、24 B、 C、 D、511. 如图,已知矩形ABCD,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )
A、24 B、 C、 D、511. 如图,已知矩形ABCD,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )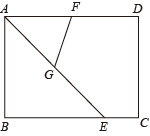 A、 B、 C、2 D、12. 如图,在中,是斜边的中线,且 , , 则的长为( )
A、 B、 C、2 D、12. 如图,在中,是斜边的中线,且 , , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,四边形是菱形, , 于点 , 则 .
 14. 在▱中, , 则 .15. 如图,在四边形中, , , 对角线 , 则线段的长为 .
14. 在▱中, , 则 .15. 如图,在四边形中, , , 对角线 , 则线段的长为 . 16. 计算: 的结果为 .
16. 计算: 的结果为 .三、解答题
-
17. 已知: , , 求代数式的值18. 若实数x,y满足 , 求的值.19. 在中, , , 边上的高 , 求另一边的长.20. 图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足 , 现测得dm,dm,dm,其中与之间由一个固定为90°的零件连接(即),通过计算说明该车是否符合安全标准.
 21. 如图,D为边上的一点, , , , , 求的长.
21. 如图,D为边上的一点, , , , , 求的长.