(人教版)云南省2023-2024学年八年级下学期期中数学模拟试卷(二)
试卷更新日期:2024-04-09 类型:期中考试
一、选择题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列二次根式中,能与 合并的是( )A、 B、 C、 D、3. 下列式子中,属于最简二次根式的是A、 B、 C、 D、4. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥15. 以下列长度的三条线段为边,能组成直角三角形的是( )A、2,3,4 B、3, , 5 C、5,12,13 D、4,4,86. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
 A、2 B、 C、 D、7. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm , 接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A、2 B、 C、 D、7. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm , 接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )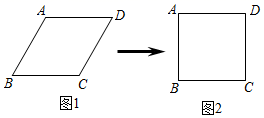 A、20cm B、30cm C、40cm D、20 cm8. 如图,是台阶的示意图.已知每个台阶的宽度都是20cm,每个台阶的高度都是10cm,连接AB,则AB等于( )
A、20cm B、30cm C、40cm D、20 cm8. 如图,是台阶的示意图.已知每个台阶的宽度都是20cm,每个台阶的高度都是10cm,连接AB,则AB等于( )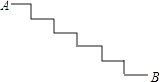 A、120cm B、130cm C、140cm D、150cm9. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( )
A、120cm B、130cm C、140cm D、150cm9. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( ) A、1 B、2 C、3 D、410. 如图,正方形中,点E、F、H分别是、、的中点,、交于G , 连接、 . 下列结论:①;②;③;④ , 其中正确的有( )
A、1 B、2 C、3 D、410. 如图,正方形中,点E、F、H分别是、、的中点,、交于G , 连接、 . 下列结论:①;②;③;④ , 其中正确的有( )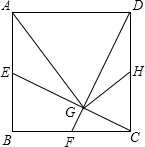 A、1个 B、2个 C、3个 D、4个11. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
A、1个 B、2个 C、3个 D、4个11. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
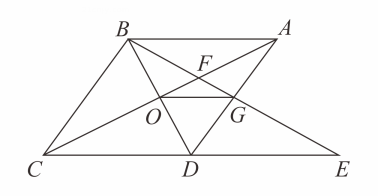
;与全等的三角形共有个;
;由点、、、构成的四边形是菱形.
A、 B、 C、 D、12. 如图,菱形中,对角线、相交于点O , H为边中点,菱形的周长为24,则的长是( ) A、3 B、 C、 D、12
A、3 B、 C、 D、12二、填空题
-
13. 化简二次根式的结果为 .14. 要使二次根式 有意义,则x的取值范围是 .15. 如图,一场暴雨过后,垂直于地面的一棵树在距地面米的点处折断,树尖恰好碰到地面,经测量米,则树高为米.
 16. 如图,已知ABCD中对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个矩形.你添加的条件是 .
16. 如图,已知ABCD中对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个矩形.你添加的条件是 .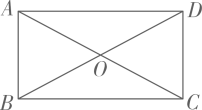
三、解答题
-
17. 先化简,再求值: , 其中满足.18. 阅读下列例题.
在学习二次根式性质时我们知道 ,
例题:求的值.
解:设 , 两边平方得:
,
即 , ,
,
,
,
请利用上述方法,求的值.
19. 某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? 20. 如图,中, , , , 于 , 求斜边和高的长.
20. 如图,中, , , , 于 , 求斜边和高的长. 21. 如图,在中, , , .
21. 如图,在中, , , .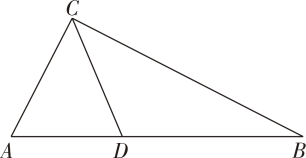 (1)、求的长度;(2)、已知是上一点,连接 , 当的长度最短时,求的长度.22. 如图所示,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证AM=EF.
(1)、求的长度;(2)、已知是上一点,连接 , 当的长度最短时,求的长度.22. 如图所示,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证AM=EF.

