(人教版)云南省2023-2024学年八年级下学期期中数学模拟试卷(一)
试卷更新日期:2024-04-09 类型:期中考试
一、选择题
-
1. 下列各式中正确的是( )A、 B、 C、 D、2. 要使二次根式有意义,则x的取值范围是( )A、 B、 C、 D、3. 下列二次根式中,与是同类二次根式的是( )A、 B、 C、 D、4. 若 与最简二次根式 是同类二次根式,则m的值为( )A、7 B、11 C、2 D、15. 我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中.下列各组数中,是“勾股数”的是( )A、 B、 C、 D、6. 如图,是等边三角形,边长为2,根据作图的痕迹,则的长为( ).
 A、 B、 C、 D、7. 如图,在的网格中,每个小正方形的边长均为1,点A、B都在格点上,则下列结论错误的是( )
A、 B、 C、 D、7. 如图,在的网格中,每个小正方形的边长均为1,点A、B都在格点上,则下列结论错误的是( ) A、的面积为10 B、 C、 D、点A到直线的距离是28.
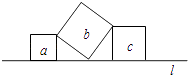
A、的面积为10 B、 C、 D、点A到直线的距离是28.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
 A、4 B、6 C、16 D、559. 如图平行四边形中,对角线相交于点 , 点E是的中点,若 , 则的长为( )
A、4 B、6 C、16 D、559. 如图平行四边形中,对角线相交于点 , 点E是的中点,若 , 则的长为( )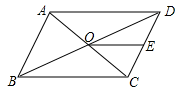 A、3 B、12 C、8 D、1010. 如图,在矩形中,对角线、相交于点 , 于点 , :: , 且 , 则的长度是( )
A、3 B、12 C、8 D、1010. 如图,在矩形中,对角线、相交于点 , 于点 , :: , 且 , 则的长度是( ) A、 B、 C、 D、11. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( )
A、 B、 C、 D、11. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( ) A、 B、 C、 D、12. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A、 B、 C、 D、12. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )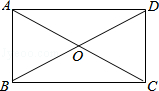 A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB
A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB二、填空题
-
13. 如果代数式有意义,那么x的取值范围是.14. 计算: × =.15. 如图,以△ABC的三边为边向外作正方形,其面积分别为S1 , S2 , S3 , 且S1=9,S3=25,当S2=时∠ACB=90°.
 16. 如图,在平行四边形中, , 的平分线交于点E,交的延长线于点F,则cm.
16. 如图,在平行四边形中, , 的平分线交于点E,交的延长线于点F,则cm.
三、解答题
-
17. 已知: , , 求:的值.18. 【知识再现】乘积为1的两个数互为倒数.如: , 我们就说2和互为倒数.
【主题探究】在学习二次根式的过程中,某数学兴趣小组发现有一些特殊无理数之间也具有互为倒数的关系.例如: , 可得与互为倒数.
即 , .
类似的, , , , .
【启发应用】请根据以上规律,解决下列问题:
(1)、 , ;(为正整数)(2)、若 , 则=;(3)、计算: .19. 小明家装修,电视背景墙长BC为m,宽AB为m,中间要接一个长为m,宽为m的大理石图案(图中阴影部分),除去大理石图案部分,其他部分贴壁布,求壁布的面积.(结果化为最简二次根式) 20. 《西江月》中描述:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…;翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺)将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索的长度.
20. 《西江月》中描述:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…;翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺)将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索的长度.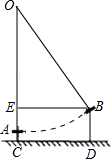 21. 如图,在四边形中, , , , , . 求四边形的面积.
21. 如图,在四边形中, , , , , . 求四边形的面积. 22. 如图,证明定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
22. 如图,证明定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.已知:点、分别是的边、的中点.
求证: , .


