(人教版)云南省2023-2024学年七年级下学期期中数学模拟试卷(一)
试卷更新日期:2024-04-09 类型:期中考试
一、选择题
-
1. 如图,直线a,b相交, , 则的度数为( )
 A、 B、 C、 D、2. 9的平方根是( )A、3 B、 C、 D、3. 下列现象中,不属于平移的是( )A、滑雪运动员在平坦的雪地上沿直线滑行 B、时针的走动 C、商场自动扶梯上顾客的升降运动 D、火车在笔直的铁轨上行驶4. 在平面直角坐标系中,点P( , 2)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,要把河中的水引到村庄A,小凡先作AB⊥CD,垂足为点B,然后沿AB开挖水渠,就能使所开挖的水渠最短,其依据是( )
A、 B、 C、 D、2. 9的平方根是( )A、3 B、 C、 D、3. 下列现象中,不属于平移的是( )A、滑雪运动员在平坦的雪地上沿直线滑行 B、时针的走动 C、商场自动扶梯上顾客的升降运动 D、火车在笔直的铁轨上行驶4. 在平面直角坐标系中,点P( , 2)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,要把河中的水引到村庄A,小凡先作AB⊥CD,垂足为点B,然后沿AB开挖水渠,就能使所开挖的水渠最短,其依据是( ) A、两点确定一条直线 B、两点之间线段最短 C、直线外一点与直线上各点连接的所有线段中,垂线段最短 D、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线6. 把一副三角尺按如图所示的方式摆放,使 FD∥BC.若点 E 恰好落在 CB的延长线上,则∠BDE的度数为( )
A、两点确定一条直线 B、两点之间线段最短 C、直线外一点与直线上各点连接的所有线段中,垂线段最短 D、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线6. 把一副三角尺按如图所示的方式摆放,使 FD∥BC.若点 E 恰好落在 CB的延长线上,则∠BDE的度数为( )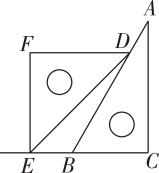 A、10° B、15° C、25° D、30°7. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A、10° B、15° C、25° D、30°7. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )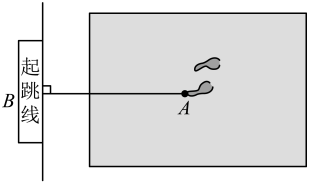 A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直8. 下列图形中,和是同位角的是( )A、
A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直8. 下列图形中,和是同位角的是( )A、 B、
B、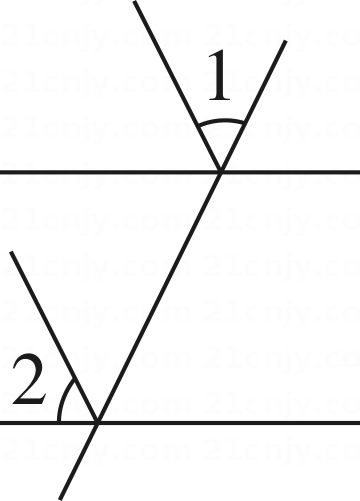 C、
C、 D、
D、 9. 如图,过直线外一点画已知直线的平行线的方法,其依据是( )
9. 如图,过直线外一点画已知直线的平行线的方法,其依据是( ) A、同旁内角互补,两直线平行 B、两直线平行,同位角相等 C、同位角相等,两直线平行 D、内错角相等,两直线平行10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )
A、同旁内角互补,两直线平行 B、两直线平行,同位角相等 C、同位角相等,两直线平行 D、内错角相等,两直线平行10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( ) A、 B、 C、α+β=γ D、11. 如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是( )
A、 B、 C、α+β=γ D、11. 如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是( )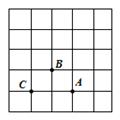 A、(1,0) B、(1,2) C、(2,1) D、(1,1)12. 按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( )
A、(1,0) B、(1,2) C、(2,1) D、(1,1)12. 按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( ) A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
13. 如图,直线a,b被直线c所截,则∠2的内错角是 .
 14. 的平方根是 .15. 在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是 .16. 把命题“对顶角相等”改写成“如果…那么…”的形式:
14. 的平方根是 .15. 在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是 .16. 把命题“对顶角相等”改写成“如果…那么…”的形式:三、解答题
-
17. 如图,直线、 , 相交于点O, , , 求的度数以及的度数.
 18. 如图,点F 在线段AB上,点E,G在线段CD 上,FG∥AE,∠1=∠2.
18. 如图,点F 在线段AB上,点E,G在线段CD 上,FG∥AE,∠1=∠2.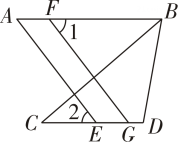 (1)、试说明:AB∥CD.(2)、若BC平分∠ABD,∠D=112°,求∠C的度数.19. 如图,点在直线上, , .
(1)、试说明:AB∥CD.(2)、若BC平分∠ABD,∠D=112°,求∠C的度数.19. 如图,点在直线上, , .求证: .
 20. 先阅读然后解答提出的问题:
20. 先阅读然后解答提出的问题:设a、b是有理数,且满足 , 求ba的值.
解:由题意得 ,
因为a、b都是有理数,所以a-3,b+2也是有理数,
由于是无理数,所以a-3=0,b+2=0,
所以a=3,b=-2, 所以 .
问题:设x、y都是有理数,且满足 , 求x+y的值.
21. 大家都知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是 , 将这个数减去其整数部分,差就是小数部分.请解答:(1)、的整数部分为 , 小数部分可以表示为;(2)、已知: , 其中是整数,且 , 请你帮忙确定一下的相反数的值.22. 已知:实数、、在数轴上的位置如图:且 , 化简:.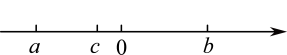 23. 如图是天安门广场周围的主要景点分布示意图,在此图中建立平面直角坐标系,表示故宫的点坐标为 , 表示美术馆的点的坐标为 , 并写出其余各个景点的坐标.
23. 如图是天安门广场周围的主要景点分布示意图,在此图中建立平面直角坐标系,表示故宫的点坐标为 , 表示美术馆的点的坐标为 , 并写出其余各个景点的坐标.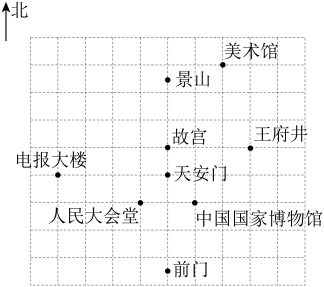 24. 阅读与理解:
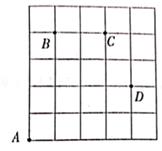
24. 阅读与理解:如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“-”,并且第一个数表示左右方向,第二个数表示上下方向。
例如:从A到B记为:A→B(+1,+4),
从D到C记为:D→C(-1,+2)。
思考与应用:
(1)、图中A→C( , );B→C( , );
D→A( , )。
(2)、若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,-2),请在图中标出P的位置。(3)、若甲虫的行走路线为A一(+1,+4)→(+2,0)→(+1,-2)-(-4,-2),请计算该甲虫走过的总路程。