人教版初中数学2023-2024学年八年级下学期课时培优练习 18.2特殊的平行四边形
试卷更新日期:2024-04-08 类型:同步测试
一、选择题
-
1. 如图,在矩形ABCD中,O为AC的中点,过点O作AC的垂线,分别交DC于点F,交AB于点E,G是AE的中点,且∠AOG=30°,有下列结论:①DC=3OG;②OG=BC;③连结AF,CE,四边形AECF为菱形;④其中正确的是( )
 A、②③ B、③④ C、①②④ D、①③④2. 如图,矩形中,为的中点,过点的直线分别与 , 交于点 , , 连接交于点 , 连接 , . 若 , , 则下列结论:① , ;②;③四边形是菱形;④ . 其中正确结论的个数是( )
A、②③ B、③④ C、①②④ D、①③④2. 如图,矩形中,为的中点,过点的直线分别与 , 交于点 , , 连接交于点 , 连接 , . 若 , , 则下列结论:① , ;②;③四边形是菱形;④ . 其中正确结论的个数是( ) A、1 B、2 C、3 D、43. 如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P , 使△PBE的周长最小,则△PBE的周长的最小值为( )
A、1 B、2 C、3 D、43. 如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P , 使△PBE的周长最小,则△PBE的周长的最小值为( ) A、2+2 B、4 C、4 D、64. 如图,在中, , , , 点为边上一动点,于 , 于 , 点为中点,则的最小值为( )
A、2+2 B、4 C、4 D、64. 如图,在中, , , , 点为边上一动点,于 , 于 , 点为中点,则的最小值为( ) A、 B、 C、 D、5. 在正方形中,点E、F在对角线上, , 若点E、F是的三等分点,点P在正方形的边上从点A开始按逆时针方向运动一周,直至返回点A,则此过程中满足为整数的点P个数为( )
A、 B、 C、 D、5. 在正方形中,点E、F在对角线上, , 若点E、F是的三等分点,点P在正方形的边上从点A开始按逆时针方向运动一周,直至返回点A,则此过程中满足为整数的点P个数为( )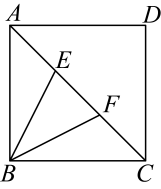 A、38 B、36 C、20 D、226. 如图,在正方形中,已知点是线段上的一个动点(点与点不重合),作交于点 . 现以 , 为邻边构造平行四边形 , 连接 , 则的最小值为( )
A、38 B、36 C、20 D、226. 如图,在正方形中,已知点是线段上的一个动点(点与点不重合),作交于点 . 现以 , 为邻边构造平行四边形 , 连接 , 则的最小值为( ) A、 B、 C、 D、7. 如图,以直角三角形的斜边为边在三角形的同侧作正方形 , 正方形的对角线 , 相交于点 , 连接 , 如果 , , 则正方形的面积为( )
A、 B、 C、 D、7. 如图,以直角三角形的斜边为边在三角形的同侧作正方形 , 正方形的对角线 , 相交于点 , 连接 , 如果 , , 则正方形的面积为( ) A、20 B、22 C、24 D、268. 如图,在平行四边形中,、分别为边、的中点,是对角线, , 交的延长线于 , 连接 , 若 . 下列结论:①;②四边形是菱形;③;④ . 其中正确的是( )
A、20 B、22 C、24 D、268. 如图,在平行四边形中,、分别为边、的中点,是对角线, , 交的延长线于 , 连接 , 若 . 下列结论:①;②四边形是菱形;③;④ . 其中正确的是( ) A、①②③④ B、①②③ C、①②④ D、①③④9. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形与正方形 , 点O为对角线的中点,过点O,分别交 , 于点M,N,若 , , 连 . 则的值为( )
A、①②③④ B、①②③ C、①②④ D、①③④9. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形与正方形 , 点O为对角线的中点,过点O,分别交 , 于点M,N,若 , , 连 . 则的值为( ) A、 B、 C、 D、10. 如图,在正方形ABCD中,延长DC至点 , 以CG为边向下画正方形CEFG.延长AB交边FG于点 , 连结CF,AF分别交AH,CE于点 , , 在清朝四库全书的《几何通解》中,利用此图得到了:.若 , 且正方形ABCD与CEFG的面积之和为68,则AH的长为( )
A、 B、 C、 D、10. 如图,在正方形ABCD中,延长DC至点 , 以CG为边向下画正方形CEFG.延长AB交边FG于点 , 连结CF,AF分别交AH,CE于点 , , 在清朝四库全书的《几何通解》中,利用此图得到了:.若 , 且正方形ABCD与CEFG的面积之和为68,则AH的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为.
 12. 如图,定义:若菱形 AECF 与正方形ABCD的两个顶点A,C重合,另外两个顶点E,F在正方形ABCD 的内部,则称菱形AECF 为正方形ABCD 的内含菱形.若正方形的周长为16,其内含菱形的边长是整数,则内含菱形的周长为;若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为.
12. 如图,定义:若菱形 AECF 与正方形ABCD的两个顶点A,C重合,另外两个顶点E,F在正方形ABCD 的内部,则称菱形AECF 为正方形ABCD 的内含菱形.若正方形的周长为16,其内含菱形的边长是整数,则内含菱形的周长为;若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为. 13. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 .
13. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 . 14. 如图,矩形ABCD中,AB=2,AD=4,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是.
14. 如图,矩形ABCD中,AB=2,AD=4,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是. 15. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .
15. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .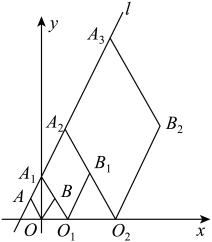
三、解答题
-
16. 如图,在平行四边形ABCD中,AD=9 cm,CD= cm,∠B=45°,点M,N分别以A,C为起点,以1 cm/s的速度沿AD,CB边运动,设点M,N运动的时间为t s(0≤t≤6). .
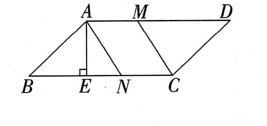 (1)、求BC边上的高AE的长度.(2)、连结AN,CM,当t为何值时,四边形AMCN为菱形?(3)、作MP⊥BC于点P,NQ⊥AD于点Q,当t为何值时,四边形MPNQ为正方形?17. 如图,在▱ABCD中,AB=6 cm,BC=10 cm,∠B=60°,G是CD的中点,E是边AD 上的动点,EG 的延长线与BC 的延长线相交于点 F,连结 CE,DF.
(1)、求BC边上的高AE的长度.(2)、连结AN,CM,当t为何值时,四边形AMCN为菱形?(3)、作MP⊥BC于点P,NQ⊥AD于点Q,当t为何值时,四边形MPNQ为正方形?17. 如图,在▱ABCD中,AB=6 cm,BC=10 cm,∠B=60°,G是CD的中点,E是边AD 上的动点,EG 的延长线与BC 的延长线相交于点 F,连结 CE,DF. (1)、求证:四边形CEDF 是平行四边形.(2)、①当AE= cm时,四边形CEDF 是菱形,请说明理由.
(1)、求证:四边形CEDF 是平行四边形.(2)、①当AE= cm时,四边形CEDF 是菱形,请说明理由.②当 AE= cm时,四边形 CEDF 是矩形,请说明理由.
18. 如图,四边形 ABCD为正方形,E 为对角线AC 上一点,连结 DE,过点 E 作EF⊥DE,交BC于点 F,以DE,EF为邻边作矩形 DEFG,连结 CG. (1)、求证:矩形 DEFG 是正方形.(2)、若 求 CG 的长.(3)、当 时,求∠EFC的度数.19. 在四边形中, , 对角线平分 , 点为边上一点,连接交于点 , .
(1)、求证:矩形 DEFG 是正方形.(2)、若 求 CG 的长.(3)、当 时,求∠EFC的度数.19. 在四边形中, , 对角线平分 , 点为边上一点,连接交于点 , .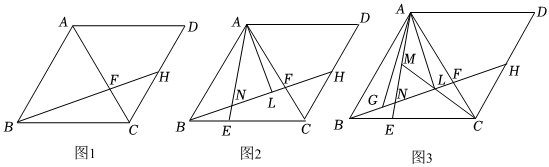 (1)、如图 , 求证:四边形是菱形;(2)、如图 , 点在上, , 交于点 , 于点 , 若 , 求证: .(3)、如图 , 在的条件下,为的中点,点在上,点在上,连接 , , , , 若 , 求线段的长,20. 如图,正方形的边都在坐标轴上,点的坐标为 , 将正方形绕点顺时针旋转 , 得到正方形 , 交线段于点 , 的延长线交线段于点 , 连接 , .
(1)、如图 , 求证:四边形是菱形;(2)、如图 , 点在上, , 交于点 , 于点 , 若 , 求证: .(3)、如图 , 在的条件下,为的中点,点在上,点在上,连接 , , , , 若 , 求线段的长,20. 如图,正方形的边都在坐标轴上,点的坐标为 , 将正方形绕点顺时针旋转 , 得到正方形 , 交线段于点 , 的延长线交线段于点 , 连接 , . (1)、求证:;(2)、求的度数;(3)、当时,求点的坐标;(4)、在(3)的条件下,直线上是否存在点 , 使以点 , 为顶点的三角形是等腰三角形?若存在请直接写出点的坐标;若不存在请说明理由.
(1)、求证:;(2)、求的度数;(3)、当时,求点的坐标;(4)、在(3)的条件下,直线上是否存在点 , 使以点 , 为顶点的三角形是等腰三角形?若存在请直接写出点的坐标;若不存在请说明理由.